You are here
Journal Club for April 2017: Multiscale and Multiphysics Simulation of Hydraulic Fracturing of Gas Tight Shale
Multiscale and Multiphysics Simulation of Hydraulic Fracturing of Gas Tight Shale
Congrui Jin1 , Weixin Li2 and Gianluca Cusatis3
1 Department of Mechanical Engineering, State University of New York at Binghamton, Binghamton, NY 13902 Email: cjin@binghamton.edu
2 Theoretical and Applied Mechanics, Northwestern University, Evanston, IL 60208 Email: weixinli2013@u.northwestern.edu
3 Department of Civil and Environmental Engineering, Northwestern University, Evanston, IL 60208 Email: g-cusatis@northwestern.edu
Shale, the sealing formations in most hydrocarbon reservoirs, is made of highly compacted clay particles of sub-micrometer size, nanometric porosity and different mineralogy. It is probably one of the most complicated and intriguing natural material present on earth. The multiphase composition is permanently evolving over various scales of length and time, creating in the course of this process the most heterogeneous class of materials in existence. The heterogeneities manifest themselves from the nanoscale to the macroscopic scale, which all contribute to a pronounced anisotropy and large variety of macroscopic behavior.
The multiscale structure model, as shown in Fig. 1, provides a consistent framework for separating the length scales that are most relevant to our research. The formulation of a multiscale simulation model requires three fundamental ingredients: (1) mathematical formulation describing the behavior of interest at a certain given scale; (2) experimental and field observations for the purpose of calibration and validation; and (3) multiscale theories and technologies allowing the upscaling of the selected model to Scale 1. Since the goal of our research is to obtain theories and models to be used at Scale 1 for practical applications, we establish the length scales of interest to be that of an intact rock specimen at the centimeter scale and higher, i.e., from Scale 4 to Scale 1. Other finer scales defined all the way down to the atomic structure are not scales of our interest.

Figure 1: Shale multi-scale structure model.
Scale 4 corresponds to that of a typical laboratory specimen used in standard mechanical characterization experiments such as acoustic measurements for elasticity and triaxial testing for strength properties. As a result of sediment transport by a variety of processes, many shale specimens exhibit mm- and cm-scale grain-size variability, lamination, bedding planes, scour surfaces, and burrows, which play a significant role in shale geo-mechanical characteristics, such as the degree of anisotropy, tensile strength and fracture toughness.
Because of shale’s unique and very intricate geological, physical, and mechanical properties compared with sandstones and carbonates, the adjective “unconventional” has often been applied to their characterization. Despite the remarkable interest in their properties, the current literature on reservoir modeling exhibits considerable gaps. The research community is still hampered by the lack of capabilities in dealing with inherent and emergent heterogeneities, as well as to quantify the effects of the microstructure on failure events. At present, there are no convincing mechanical methodologies able to predict meso-scale phenomena, capture the evolution of heterogeneities, and use this information to derive microstructural continuum models for reservoir engineering.
A model naturally accounting for material heterogeneity is the Lattice Discrete Particle Model (LDPM) recently developed to simulate the meso-structure of quasi-brittle materials1,2. Along with its predecessor, the confinement-shear lattice model3-5, LDMP adopts constitutive laws analogous to those of the microplane model6. LDPM has been extensively calibrated and validated under a wide range of quasi-static and dynamic loading conditions, showing superior capabilities in predicting qualitative and quantitative behavior of quasi-brittle materials1,2,7-10. To simulate shale, LDPM has been significantly modified as described below.
To translate the highly heterogeneous nature of shale into a predictive model of the mechanical properties, the meso-scale response of shale is simulated by a 3D assemblage of polyhedral cells. The strategy adopted in LDPM to replicate the grain-scale heterogeneity of shale is schematically depicted in Fig. 2, which illustrates through a simplified 2D representation the basic steps required to map the real microstructure of a granular rock into its numerical analogue. As the grains in shale tend to be closely packed and in direct contact with each other11, a simplification is adopted here to discretize the material domain into a granular lattice system without the isolation of cement bridges and grains, which implies that the contribution of the cementing phase will not be modeled explicitly, but rather it will be embedded implicitly into the particle-scale constitutive laws controlling the interaction between skeletal grains.
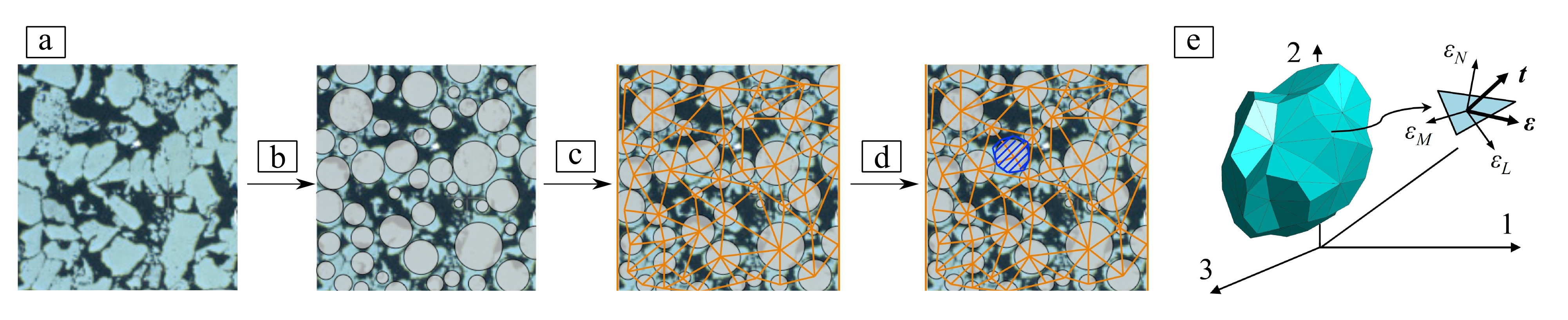
Figure 2. (a) Optical microscopy and scanning electron microscopy reveal microstructure of a shale: a porous granular fabric with the grain size ranging from 30 to 100 µm as well as micron-sized air voids. This figure is modified from Ref. 11 (Akono and Kabir, 2016). (b) An artificial supporting system with spherical particles placed at the center of shale grains is generated following a strategy similar to that proposed by Ref. 1 (Cusatis et al., 2011). (c) The Delaunay tetrahedralization discretizes the domain of interest by a 3D mesh of tetrahedra with the vertices coinciding with the given particle centers. (d) The 3D domain tessellation, anchored to the Delaunay tetrahedralization, creates a system of polyhedral cells. (e) By collecting all facets associated with a particle, one can obtain a polyhedral cell representing a cement-coated grain. This procedure has proven itself to be very effective in producing particle systems that model well the geometrical features of the response of heterogeneous solids, such as grain interlocking.
The tessellation procedure makes use of well-established packing algorithms for no-contact spherical particle placement, Delaunay triangulation of the particle centers, and non-overlapping volume tessellation by constructing a dual tessellation of the triangulated domain, which defines the surfaces through which interaction forces are exchanged between particles. The use of polyhedral particles, as opposed to spherical ones characterizing all the existing models, is instrumental for accurately reproducing the fine geometrical features of cracks, slip planes, and shear bands in quasi-brittle materials.
As a result of sediment transport by a variety of processes, a significant feature of many shale specimens at the meso-scale is the naturally formed laminae, which are planes of weakness that play a significant role in shale geomechanical characteristics, such as the degree of anisotropy, tensile strength and fracture toughness12-15. Hence, the meso-scale response of shale will be simulated by a laminated structure model with multiple layers of weakness embedded in a stiffer, stronger, and tougher matrix. In addition to explicitly simulating the weak layers, transverse isotropy in the clay matrix is also introduced, and the plane of isotropy is assumed to coincide with the plane of lamination. Different material properties will be assigned to the weak layers and the matrix accordingly, as shown in Fig. 3.
In both the weak layers and the matrix, the polyhedral particles interact through triangular facets1.Stress and strain vectors are defined at each single facet of the polyhedral cells. Discrete compatibility equations are formulated through the relative displacements and rotations of adjacent particles. Discrete equilibrium equations are obtained through equilibrium of each discrete cell.
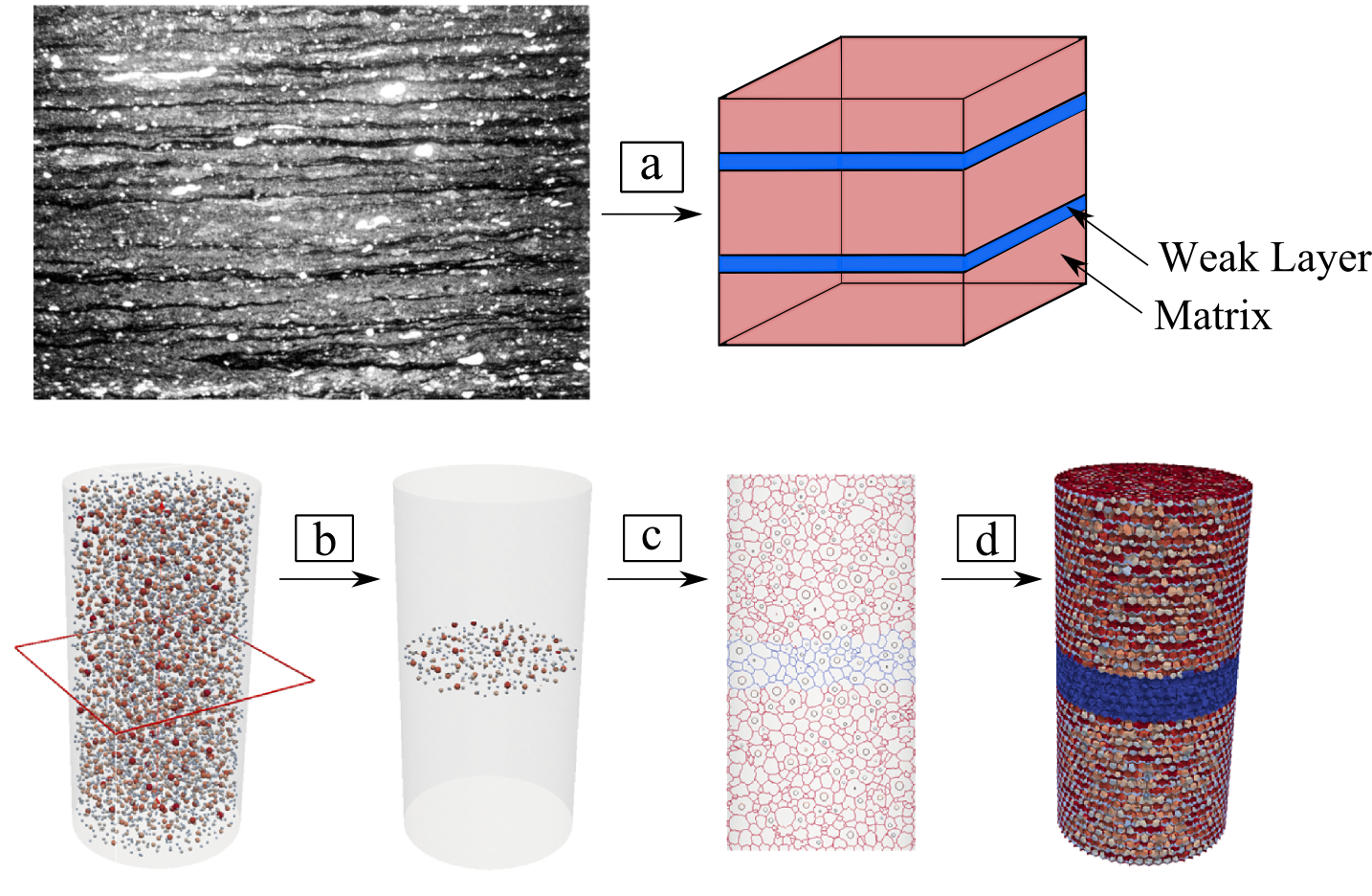
Figure 3. (a) A laminated structure model with multiple layers of weakness is used to represent a typical laminated shale. This figure is modified from Ref. 14 (Bramlette, 1946). (b) Grains located in the weak layers are first selected. (c) The facets associated with the grains are then selected. (d) Different material properties are assigned to the weak layers and the matrix accordingly.
A vectorial constitutive law is imposed at the centroid of each facet. The elastic behavior is described by assuming that the normal and shear stresses are proportional to the corresponding strains. To take into account the observed strong anisotropy of the clay matrix due to the partial alignment of anisotropic clay minerals, LDPM will be extended to simulate transversely isotropic materials by using orientation-dependent stiffnesses on each facet. The effect of weak layers will be considered by introducing reduction factors for the stiffnesses in the weak layers.
For stresses and strains beyond the elastic limit, the meso-scale failure is characterized by three mechanisms1: fracture and cohesion due to tension and tension-shear; friction due to compression-shear; and compaction and pore collapse from compression. Similar to the elastic case, to simulate transversely isotropic materials, the meso-scale parameters for inelastic behavior will also depend on the facet’s orientation angle, and reduction factors will be introduced for the region of weak layers.
To predict the macroscopic behavior of shale, “full” microscopic simulations are too expensive to perform even with the computational power currently available. This problem will be addressed by adopting a general up-scaling computational theory16 based on the classical asymptotic expansion homogenization approach17-20. This theory is built on two major assumptions. (a) There exists a certain volume of material, the so called Representative Volume Element (RVE), which properly describes the internal structure of the material under investigation. And (b) the size of the RVE is much smaller than the characteristic size of the macroscopic problem, namely the “separation of scales” hypothesis holds. This development will break the barrier of computer memory limitation and become the enabling technology that unlocks the door to large-scale simulations of fine-grained rocks accounting for microscopic heterogeneity.
Elastic microplane formulation for transversely isotropic materials has been developed by our groups21, which can be directly implemented into the LDPM framework. A general multiscale framework for the simulation of the mechanical behavior of shale has also been developed22. The model is calibrated by conducting numerical simulations to match the experimental data from the existing literature. It has been shown that the dependence of elastic stiffness, strength, and failure mode on loading orientation can be captured successfully. The homogenization approach based on the asymptotic expansion of field variables is applied to up-scale the micromechanical model. Some results are shown in Fig. 4.
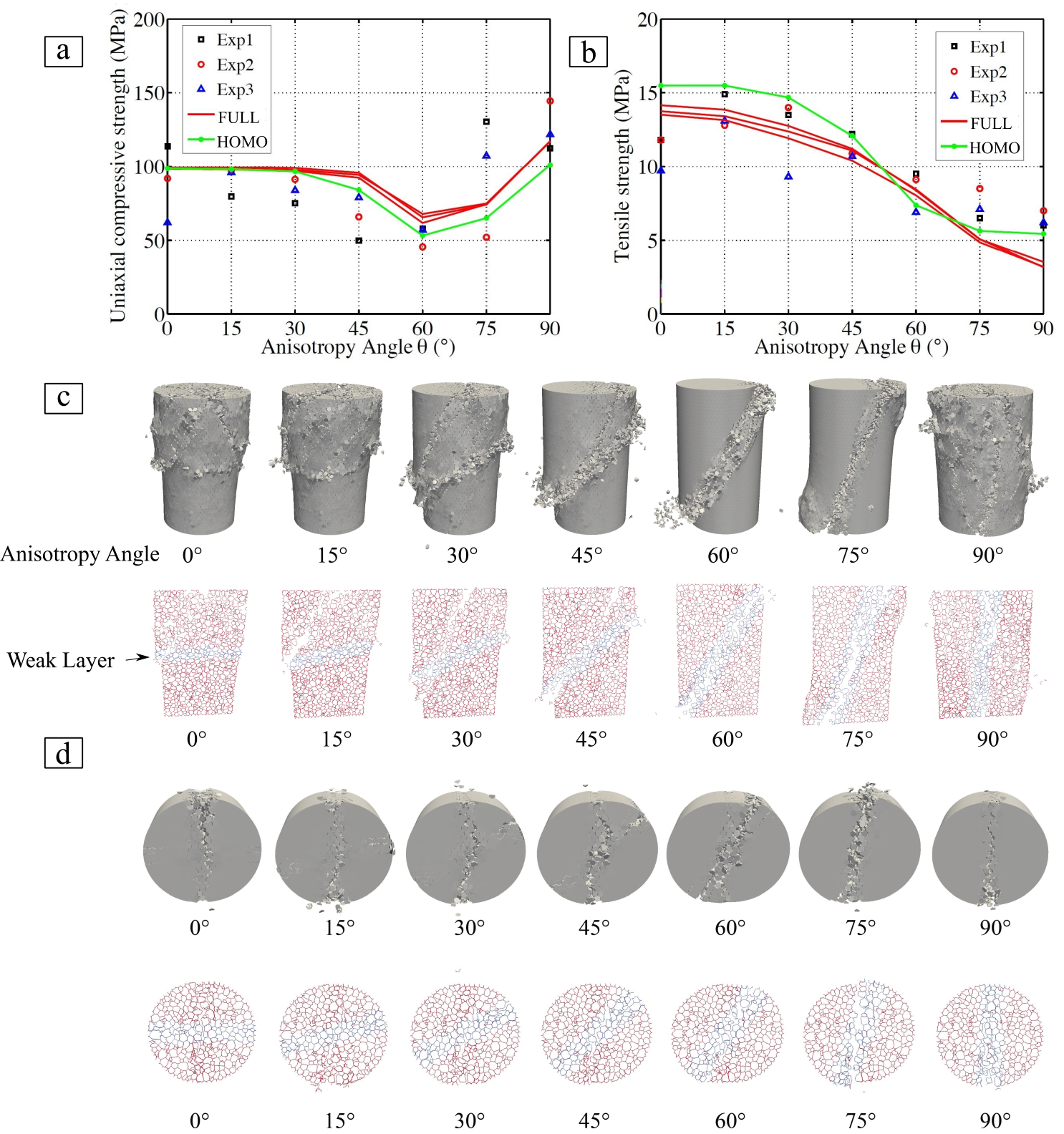
Figure 4. Comparison of (a) uniaxial compressive strength and (b) tensile strength between experimental data from the existing literature and simulation results as a function of anisotropy angle. The anisotropy angle is defined as the angle between the loading direction and the normal vector to the lamination plane. The results from both the full fine-scale simulation and the homogenization approach using a two-scale finite element method (FEM) model match the experimental data. Simulated specimens after failure for (c) uniaxial compression test and (d) Brazilian test. The snapshot of the external faces and the slice view of the simulated specimens are both shown. This figure is modified from Ref. 22 (Li et al., 2016).
References:
[1] Cusatis, G., Pelessone, D., Mencarelli, A. Lattice discrete particle model (LDPM) for failure behavior of concrete. I: Theory. Cem. Concr. Compos. 2011; 33: 881-890. http://www.sciencedirect.com/science/article/pii/S0958946511000345
[2] Cusatis, G., Pelessone, D., Mencarelli, A., Baylot, J. Lattice discrete particle model (LDPM) for failure behavior of concrete. II: Calibration and validation. Cem. Concr. Compos. 2011; 33: 891-905. http://www.sciencedirect.com/science/article/pii/S0958946511000333
[3] Cusatis, G., Bazant, Z.P., Cedolin, L. Confinement-shear lattice model for concrete damage in tension and compression: I. theory. Journal of Engineering Mechanics 2003; 129: 1439-1448.
[4] Cusatis, G., Bazant, Z.P., Cedolin, L. Confinement-shear lattice model for concrete damage in tension and compression: II. computation and validation. Journal of Engineering Mechanics 2003; 129: 1449-1458.
[5] Cusatis, G., Bazant, Z.P., Cedolin, L. Confinement-shear lattice CSL model for fracture propagation in concrete. Computer methods in applied mechanics and engineering 2006; 195: 7154-7171.
[6] Bazant, Z.P., Caner, F.C., Carol, I., Adley, M.D., Akers, S.A. Microplane model M4 for concrete. I: Formulation with work-conjugate deviatoric stress. Journal of Engineering Mechanics 2000; 126: 944-953.
[7] Smith, J., Cusatis, G., Pelessone, D., Landis, E., O’Daniels, J., Baylot, J. Lattice Discrete Particle Modeling of ultra high-performance fiber-reinforced concrete for projectile penetration simulations. International Journal of Impact Engineering 2014; 65: 13-32.
[8] Schauffert, E.A., Cusatis, G. Lattice discrete particle model for fiber-reinforced concrete. I: Theory. J. Eng. Mech. 2012; 138: 826-833.
[9] Schauffert, E.A., Cusatis, G., Pelessone, D., O’Daniel, J., Baylot, J. Lattice Discrete Particle Model for fiber reinforced concrete (LDPM-F): II Tensile fracturing and multiaxial loading behavior. J. Eng. Mech. 2012; 138: 834-841.
[10] Jin, C., Buratti, N., Stacchini, M., Savoia, M., Cusatis, G. Lattice Discrete Particle Modeling of fiber reinforced concrete: experiments and simulations. European Journal of Mechanics A/Solids 2016; 57: 85-107.
[11] Akono, A.T., Kabir, P. Microscopic fracture characterization of gas shale via scratch testing. Mechanics Research Communications 2016; In Press
[12] Slatt, R.M., Abousleiman, Y. Merging sequence stratigraphy and geomechanics for unconventional gas shales. The Leading Edge 2011; 30: 274-282.
[13] Sone, H., Zoback, M.D. Mechanical properties of shale-gas reservoir rocks. Part 1: Static and dynamic elastic properties and anisotropy. Geophysics 2013; 78: D381-D392.
[14] Bramlette, M.N. The Monterey formation of California and the origin of its siliceous rocks. U.S. Geol. Surv. Prof. Paper 1946; 212: 1-57. http://pubs.er.usgs.gov/publication/pp212.
[15] Vernik, L., Nur, A. Ultrasonic velocity and anisotropy of hydrocarbon source rocks. Geophysics 1992; 57: 727-735.
[16] Rezakhani, R., Cusatis, G. Asymptotic expansion homogenization of discrete fine-scale models with rotational degrees of freedom for the simulation of quasi-brittle materials. Journal of the Mechanics and Physics of Solids 2016; 88: 320-345.
[17] Forest, S., Pradel, F., Sab, K. Asymptotic analysis of heterogeneous Cosserat media. International Journal of Solids and Structures 2001; 38: 4585-4608.
[18] Chung, P.W., Tamma, K.K., Namburu, R.R. Asymptotic expansion homogenization for heterogeneous media: computational issues and applications. Composites Part A: Applied Science and Manufacturing 2001; 32: 1291-1301.
[19] Ghosh, S., Lee, K., Moorthy, S. Two scale analysis of heterogeneous elastic-plastic materials with asymptotic homogenization and Voronoi cell finite element model. Computer Methods in Applied Mechanics and Engineering 1996; 132: 63-116.
[20] Fish, J., Shek, K., Pandheeradi, M., Shephard, M.S. Computational plasticity for composite structures based on mathematical homogenization: theory and practice. Computer Methods in Applied Mechanics and Engineering 1997; 148: 53-73.
[21] Jin, C., Salviato, M., Li, W., Cusatis, G. Elastic microplane formulation for transversely isotropic materials. Journal of Applied Mechanics 2016; In Press http://bingweb.binghamton.edu/~cjin/publications/shale1.pdf
[22] Li, W., Rezakhani, R., Jin, C., Zhou, X., Cusatis, G. A multiscale framework for the simulation of the anisotropic mechanical behavior of shale. International Journal for Numerical and Analytical Methods in Geomechanics 2016; In Press http://bingweb.binghamton.edu/~cjin/publications/shale2.pdf
- Congrui Jin's blog
- Log in or register to post comments
- 10462 reads


Comments
crack deflection in heterogeneous shale stratums
Very nice post on the influence of the weak layers on the mechanical properties of shales!
Hydraulic fracturing could form complex crack networks in the shale reservoirs mainly due to shale‘s mechanical heterogeneicty. These macroscale networks transport the encapsulated gas or oil just like the tree roots absorb water in the soil. Why and how the crack network develops in the sediment rocks is one of the most important questions in shale fracking work. It is well known that shale’s heterogeneity has a tremendous influence on its mechanical properties and fracture behavior. The discussion in IMechanica is indeed timely. As demonstrated in Figure 1 of the post, shales have complicated structures in different length scales, and the centimeter scale (intact rock specimen scale) and higher scales are of interest for shale fracking practical applications. In these scales, there are many natural cracks in the shale, sealed or unsealed. These cracks also have an important influence on shale’s mechanical properties (Gale et al., 2007 & 2014; Zeng and Wei, http://www.sciencedirect.com/science/article/pii/S0020768316301378). In a recently paper, we try to tackle the crack deflection in such heterogeneous media (Zeng and Wei, http://www.sciencedirect.com/science/article/pii/S0022509616306573) and we hope the discussion may be of the interest of IMechanica readers. By extending the energy release rate ratio criterion (He and Hutchinson, 1989) for cracking deflection, we give the critical conditions when the hydraulic crack kinks into the weak interface. The analysis also demonstrates how crack-surface friction and crustal stresses influence crack deflection from the matrix of higher fracture toughness to weak planes of lower resistance to crack propagation. It shows that Mode II fracture along the weak interfaces dominates the hydraulic fracturing process.
References
Gale J F W, Laubach S E, Olson J E, Eichhubl P, Fall A. 2014. Natural fractures in shale: A review and new observations. AAPG Bulletin, 98: 2165-2216.
Gale J F W, Reed R M, Holder J. 2007. Natural fractures in the Barnett Shale and their importance for hydraulic fracture treatments. AAPG Bulletin, 91: 603-622.
He, M., Hutchinson, J.W., 1989. Crack deflection at an interface between dissimilar elastic materials. International Journal of Solids and Structures 25, 1053-1067.
Zeng X, Wei Y. 2016. The influence of crack orientation distribution on the mechanical properties of pre-cracked brittle media. International Journal of Solids and Structures, 96: 64-73.
Zeng X., Wei Y., 2017. Crack deflection in brittle media with heterogeneous interfaces and its application in shale fracking, Journal of the Mechanics and Physics of Solids 101, 235-249.
Figure 5. Model of path
Figure 5. Model of path choice of a hydraulic crack encountering a weak interface (left); It is revealed analytically that with increasing hydraulic pressure, a shale formation may sequentially undergo friction locking, mode II fracture, and mixed mode fracture, and in mode II fracture stage, crack-plane friction and crustal stress differences have no influence on the strain energy release rate ratio, i.e., crack deflection (right).