You are here
Journal Club Theme of February 2007: Computational Mechanics of Biomembranes

Lipid bilayers constitute one of the critical parts of all biological membranes, including cell membranes. A nice description of lipid bilayers and their function in biological membranes can be found here. They can be exceptionally complex and contain hundreds of different constituents, so simpler model lipid bilayers are often produced in the laboratory and studied experimentally. They form closed spheroidal structures, called liposomes, with a thickness of a few nm, and characteristic linear dimensions up to several microns. Larger such structures are usually called Giant Unilamellar Vesicles, or GUVs. Why should we care about these structures as mechanicians? For a number of reasons, the elastic properties of lipid membranes are thought to play a crucial role in governing their potential configurations. Recent experimental studies of the role of membrane curvature on domain formation in biomembranes, for example, provide testament to this notion. Images of their work are reproduced (with permission) here.
Although one could certainly debate the applicability of continuum models to structures such as these, in fact a great deal of insight has been provided by the same. Further, while molecular dynamics and other discrete methods certainly have a lot to offer toward understanding these structures, even coarse-grained methods are impractical for handling many of the length and time scales of interest in GUVs.
Not that things are much easier for continuum models! One of the main issues for simulations based on these concerns the relatively high order of even the simplest evolution equations. For example, the classical bilayer mechanics theory developed by Helfrich (see also the work of Canham and Evans) involves a bending energy that is quadratic in the principle curvatures of the membrane surface. This gives rise to Euler-Lagrange equations that are fourth-order. Proposed models for surface composition, akin to Cahn-Hilliard equations, are similarly fourth-order in the composition field. Given the complex geometry and possible configurations attainable with giant unilamellar vesicles, classical high-order finite difference and spectral methods are essentially impractical.
Classical finite-element methods are also problematic for fourth-order problems. The parent space of functions in this case is the second-order Sobolev space H2(S), which, roughly speaking, requires the use of smooth C1 shape functions on the membrane surface. With good reason, recent work by Feng and Klug (1) has moved away from classical shell finite elements and toward C1-conforming subdivision surfaces. Other recent work incorporating smooth basis functions includes that of Ayton et al. (2), who relied on a smoothed-particle hydrodynamics (SPH)-based method.
Although these approaches have their advantages, neither is capable of reasonably simulating the topology changes (e.g. sphere to toroid) required to predict equilibrium configurations in GUVs (though Ayton may claim otherwise). The only method with such capability appears to be that of Qiang Du and coworkers (3), employing a phase-field regularization of (essentially) the Canham-Helfrich-Evans biomembrane theory. This treatment is appealing, but it is not a particularly efficient approach, as it requires the use of a uniform Cartesian grid and embeds the interface within a higher-dimensional domain. Further, while their most recent work has allowed for spatial variations in elastic moduli, they have yet to couple their approach with composition dynamics.
The three papers included here for discussion are:
I recommend beginning with the Klug paper, as it provides some excellent background and a nice introduction to the bending aspects. The Ayton paper touches on the coupled chemo-mechanical aspects and the formation of domains in GUVs. It may prove a difficult read for the uninitiated, as the authors are attempting a very challenging problem. Finally, the Du paper is a very different take on this problem, and one that I believe to be of interest. I welcome discussion on these papers, and will focus my responses on the computational aspects.

deformation of 2D thin soft surfaces in a 3D setting
Not counting the biological chemistry, are we dealing these problems as the deformation of 2D thin soft surfaces in a 3D setting?
regarding deformation of 2D thin soft surfaces
Certainly modeling deformation is an end-goal. However, determining the equilibrium shapes of the membrane is an initial challenge. The Feng and Klug paper treats the membrane as a surface. So too does the Du et al. paper, but the numerical representation is quite a bit different.
Added to the challenge are constraints on surface area and enclosed volume.
constraint to penalty
In the paper by Feng and Klug, they change the "hard" constraints on area and volume to "soft" penalties in the energy for area/volume that goes away from the desired values (section 2.2.1). In a particular numerical procedure that I did some work with, changing constraints to penalties and making the penalties progressively larger (by increasing the coefficient in front of the penalty) led to the final stiffness matrix becoming progressively ill-conditioned.
1. Is this a general feature that one expects when one switches from constraints to penalties?
2. In the particular example they examine, they don't report this problem (see page 11). For the sort of numbers that usually come up in lipid bilayer problems for osmotic pressure causing volume constraint and similarly for the area constraint, is this something one needs to watch out for?
Thanks,
Kaushik
__________________________________
Kaushik Dayal
Aerospace Engineering and Mechanics
University of Minnesota
Contact Information:
http://www.aem.umn.edu/~kaushik/research/#ContactInfo
re: constraint to penalty
Kaushik,
I believe I can answer your first question, and perhaps we can get Bill Klug to comment on the second.
What you describe is indicative of a penalty method that is not variationally consistent. In such a case, in order to maintain good convergence with mesh refinement, the penalty parameter must grow much more quickly than the other terms in the matrix. Poor conditioning is the result. Many of the penalty methods that are used, unfortunately, are not variationally consistent. Nitsche's method is one exception.
Edit:
Regardless of the consistency issue, however, if one increases the penalty parameter while keeping the mesh fixed, one should also expect to see poor-conditioning of the matrix. However, it does not make sense to do this.
Alternatives include augmented-Lagrangian methods, where the penalty parameter is only used as a kernel to iterate and obtain the (true) Lagrange multipliers.
re: constraint to penalty
John,
Thanks for that information. I hadn't heard about variationally consistent penalties. Do you have a reference?
Thanks,
Kaushik
--
__________________________________
Kaushik Dayal
Aerospace Engineering and Mechanics
University of Minnesota
re: constraint to penalty
Kaushik,
I'm not sure there is a single reference that discusses the issue in detail. You are more likely to find papers that comment on the issue in brief and propose alternatives. Along these lines, see the edit to my comment above.
re: constraint to penalty
John,
Immediately below (12b) of Feng and Klug, they state that one could make the coefficients in front of the penalties arbitrarily large, to enforce the constraints as tightly as desired. Naively, that's what I'd expect. Can you elaborate a little why it does not make sense to do this if one keeps the mesh fixed, besides of course the problem with possible ill-conditioning?
Thanks again,
Kaushik
--
__________________________________
Kaushik Dayal
Aerospace Engineering and Mechanics
University of Minnesota
re: constraint to penalty
Kaushik,
Well, one certainly can do that, but it's not necessarily advisable. The poor conditioning is one issue. At some point, one should also expect a loss of accuracy in the other (non-constraint) terms that appear in the functional. It's a trade-off.
re: constraint to penalty
Hi Kaushik,
Sorry I didn't chime in earlier regarding your questions and comments. Of course you are right to expect conditioning issues when increasing the penalty parameter. Yours and John's comments are all right on the money.
In the study with Feng, we weren't all that ambitious with the constraint accuracy (if I recall, we were content to get the area and volume to within 0.1% or so), so we got away with penalty parameters which weren't too big.
By the way, in the paper we used a nonlinear conjugate gradient solver rather than a newton solver, so we didn't actually form a stiffness matrix, but for larger penalty coefficients conditioning problems did seem to be manifested in the form of slow oscillatory-like convergence of the CG method. More recently, (after finishing the paper) we've used the Augmented Lagrangian approach combined with an incremental updating of the penalty coefficient to get better accuracy when we want it. That works very nicely and still allows the CG to converge quickly. In my experience, at least for quasi-static problems, AL is definitely the way to go.
Regarding your question about realistic numbers based on osmotic pressure etc., I would say that yes one does need to be concerned about the separation of energy scales between bending and area/volume change. The forces/energies resisting stretching and volume change are several orders of magnitude larger than internal forces due to bending. This is why people usually treat those constraints as hard. In a sense, it might seem that Feng and I "cheated" a bit here by using penalty coefficients that were perhaps smaller than the measured area and volume "stiffness". However, for the particular problem that we chose to solve (shape as a function of reduced volume), the fact that the constraints aren't satisfied exactly is irrelevant since the constraint violations serve only to give you an effective pressure and tension. If you dropped the penalty terms and put in fixed Lagrange multipliers with the pressure and tension computed from the penalty terms, the shape would still be in equilibrium. At any rate, you are right to be concerned about these issues as they can be generally important for vesicle mechanics.
Best,
Bill
re: constraint to penalty
Dear Bill,
I enjoyed reading your paper very much. Thanks to you and John for the detailed replies.
Regards,
Kaushik
thanks Bill for commenting
Bill, thanks for commenting on this issue and informing folks of how you're approaching this of late. I'm sure this will be quite valuable for people working in this area.
feb journal club
john, good topic and discussion. need to catch-up on all posts. shall check out bill's paper (starting point); might have some questions down the road.
Meshfree methods and GUV simulations
I tried to approach the Giant Unilamellar Vesicle (GUV) problem a few years ago with the Material Point Method. I was trying to find out whether I could reproduce some of the the results reported by Baumgart et al., Nature, 425:821, 2003.; A couple of sample images from the paper can be seen below.
An example of a simulation of the problem from Taniguchi, PRL, 76:4444, 1996is shown below.
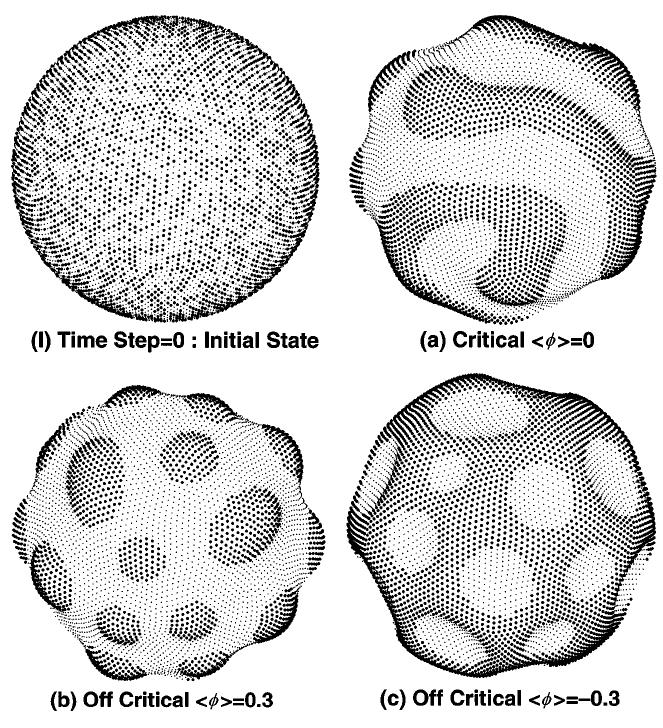
The general idea was to minimize a Ginzberg-Landau free energy functional over the
surface of the GUV and to see how the cholesterol and lipid domains interacted. However, the numerical method was not able to deal with the problem, primarily because of the absence of a grid that fit the surface. Does anyone know how well other meshfree methods do for this type of problem? (The problem I tried to simulate was a three-dimensional one with fluid-structure interaction in addition to the dynamics of cholesterol motion on the surface of the membrane.)
re: meshfree and GUV
Biswajit,
Thank you for your comment. In principle, I do not see why a meshfree method could not handle this problem. Indeed, the second paper listed above essentially uses a meshfree method. They do not appear to obtain results as interesting as those of Taniguchi, however.
Smooth Particle Applied Mechanics
Smooth Particle Applied Mechanics may be a better choice than the Material Point Method in this case.
re: SPAM
Perhaps, but it is difficult to conclude this on the basis of the above alone. I see no reason why both cannot address this problem.
Re: Particle methods and large deformations in vesicles
John and Henry,
Thank you for your comments.
In principle, given enough discretization, one should be able to predict the deformation of GUVs. However, particularly in situations such as the star-shaped GUV I showed in my previous comment, the amount of discretization that is needed becomes phohibitive.
I did interact with Gary Ayton on SPAM for a while before I realized that very large deformations cannot be handled by that method (without extremely fine discretization). I presume that a similar restriction will exist for other particle methods. I wonder how small the support of each particle would have to be to accurately represent the S-shaped bends.
Surface mesh based Galerkin methods are clearly advantageous for these problems, even though interaction with a surrounding fluid may not be as straightforward to implement as for the material point method.
re: large deformation and particle methods
Biswajit,
In fact, SPAM is based on SPH, a meshfree method that is designed to handle large deformations. However, SPH does not do very well when material strength is involved, and exhibits a well-known tensile instability. I wonder if this is what you saw with SPAM.
Regardless, your comment concerning the star-shaped profiles is absolutely correct. In this case, the SPAM particles would have to be closely packed to represent the geometry well and not have supports artificially interact. The packing may be such that single-processor calculations are no longer an option. Perhaps this is what you meant by prohibitive?
predictor-corrector step in Du, Liu and Wang
In the final discretized evolution equation derived by Du et al, (3.18), the system of equations seems to be an algebraic nonlinear coupled (coupling the field variable \phi at each grid point) system that is to be solved at each time-step.
The authors use a "predictor-corrector" to solve this system (3.18), see end of Section 3.1. I wasn't sure what a predictor-corrector means in this context. A CFD researcher showed me a way to solve it using what is called by them a "fractional step method". Does somebody with knowledge of both these methods know if they are the same thing?
Re: predictor-corrector
I'd suspect the two terms are synonymous; just saw the section in question and here's how I see it. In solids, predictor-corrector terminology is more prevalent (elastic-predictor, plastic-corrector in plasticity), and in essence conveys that for an update f_n -> f_n+1 one needs a two-step process (first compute a predictor and then fix it via the corrector step since the former might not meet any constraints that must be satisfied.) There are of course more details in between. In fluids, fractional step methods are typically used to solve the incompressible Navier-Stokes equations (I think this goes back to Chorin's work in the late 60s). From the momentum equation, an approximation for the velocity is obtained (in general this will not be divergence-free). Then, a scalar (pressure/pressure-correction) Poisson equation is solved with the divergence of the velocity field on the right-hand side. The gradient of this pressure/pressure-correction is used to form the correction on the velocity approximation to obtain a divergence-free velocity field. This closes the loop.
Re: predictor-corrector
Thanks for the clarification Sukumar.
Subdivision
A few questions and comments. 1. For the membrane problem, is the implementation a tad easier than other subdivision FE applications (due to essential bcs, ghost nodes and/or Lagrange multipliers are needed since subdivision surfaces do not interpolate)? In principle, any C^1 approximant would work, but the nodal basis function supports are `nice' (2-rings of a node) for subdivision and hence integration (3-point) is not a major issue; 2. Was the choice of CG/line-search due to the fact that the functional in (12b) is not strictly convex and hence CG was preferred over Newton (Hessian computation)? 3. Results with subdivision are super-good (just 160 nodes on a sphere). Are these reasonably converged solutions (not much change with more refinement)? 4. If both the starting area (smaller sphere) and reduced volume are off would one still converge to the same local minima? Is it possible to convexify the problem somehow by modifying the functional of interest (i am thinking of the epigraph)?