You are here
Journal Club for November 2022: Entropy-driven mechanics of crystalline and biological membranes
Fatemeh Ahmadpoor
New Jersey Institute of Technology
Linking the continuum concepts to the microscopic characteristics of materials has been an old topic of interest for both mechanics and physics communities. While the starting point for a typical continuum mechanics model is a very well-defined reference configuration of a structure, at the atomic level, the materials do not always appear undeformed and static and even solid materials constantly experience random deformations--- known as thermal fluctuations--- purely due to the thermal energy. When these thermal fluctuations are comparable with at least one of the length-scale of a nanostructure they can impact its mechanical and physical properties.
In this J-club, I would like to review a brief summary of implications of thermal fluctuations in mechanics of biological and crystalline membranes--- as a class of flexible nanostructures, with large thermal fluctuations--- as well as technical challenges for implementing them in mechanical modeling of these structures.

Biological membranes ---lipid bilayers--- are considered the Nature's flexible nanostructures due to their very small thickness (~4 nm), that governs cell's viability and functionality through mechanical deformations. In the realm of man-made flexible nanostructures, crystalline membranes such as molybdenum disulphide, phosphorene, boron nitride and MXenes---to name a few--- are fascinating for numerous reasons. Their geometrical and mechanical characteristics along with other associated physical properties have opened up tantalizing new application avenues such as nanosensors, nanoresonators, biomedical devices, gene therapy, electronics, energy harvesting, structural composites among others [1-4]. From the mechanics point of view, both biological and crystalline membranes are modeled as elastic sheets, with two unique characteristics: they are extremely flexible and bend easily and at the same time very hard to stretch. Thus, bending deformations are their dominant mode of response to any external stimuli. Typical bending modulus κb of most lipid-bilayers is between 5 and 25 kBT—small enough compared to the thermal energy scale that membranes undulate or fluctuate noticeably at physiological temperatures. Bending rigidity of a simple crystalline membrane such as graphene at zero Kelvin, has been estimated to range from 1.2 to 1.6 eV [5-7], just a few times larger than the bending rigidity of biological membranes (at room temperature). Thus, the energy cost for bending deformations of these structures is typically very low and at finite temperature, thermal undulations--- also known as thermal rippling--- are well-evident.
Extracting mechanical properties from thermal fluctuations
Thermal fluctuations spectra, provides a unique route to extract mechanical properties of both biological and crystalline membranes. Mechanical properties of membranes are typically listed as bending moduli, surface tension, Youngs modulus and edge properties. For a brief summary on how to relate these properties to fluctuations spectra, I'd like to invite you to check out these references [8-11].
Fluctuations spectra is commonly used to extract the bending modulus of biological membranes from simulations or experimental data. The fluctuations spectra have been also extended to other contexts providing a novel route to extract useful information about membranes e.g. the incorporation of electromechanical coupling [12], tilt of lipids [13, 14], presence of heterogeneities [15-17], proximity to substrates or other vesicles [18, 19] among others. For solid membranes such as graphene, however, a closed form theoretical expression for the fluctuation spectra is not possible due to nonlinearities arising from coupling of in and out-of-plane deformations [8,9]. The kinematic of deformation for solid membranes is quite similar to von-Karman nonlinear plate theory. In this case, the fluctuation data gives us the "effective"--- and not the "bare"--- value for the bending stiffness which is found to be both size and temperature dependent [9, 10].
The estimation of the Gaussian modulus of membranes, on the other hand, is quite difficult. The thermal fluctuation spectra result is independent of the Gaussian modulus. This is a consequence of a more general principle---the so-called Gauss-Bonnet theorem which states that the integration of the Gaussian curvature over a closed surface is invariant under any deformation that is not involved with topological transformations. To quote Hu et. al. [13], this is both a blessing and a curse. That is why, we can safely ignore the contribution due to the Gaussian curvature in several practical situations unless there is a change in topology. However, due to this very reason, Gaussian modulus is notoriously difficult to measure. To understand this, it is worthwhile to mention some of the physical processes where it does matter: pore formation, structural deformation of a finite ribbon, cellular uptake of nanoparticles, cell fusion and fission are some examples. However, there are no clear experimental procedures that can readily use these aforementioned events to estimate this elusive material property. In a recent work [11], recognizing that the Gaussian modulus and edge tension play a non-trivial role in the fluctuations of an open edge, a closed-form expression for edge fluctuations is derived and combined with atomistic simulations, used to extract Gaussian modulus and edge tension at finite temperature for both graphene and various types of lipid bilayers. Of course, the methodology could be applied to any other biological and crystalline membranes.
Entropic pressure plays critical role in interaction of flexible nanostructures with other materials.

Many physiological processes are involved with thermal fluctuations such as exo and endo-cytosis, membrane fusion, pore formation, cell adhesion, binding-unbinding transitions, self assembly, vesicle size distributions, the configuration of red blood cell membranes and cytoskeleton and actin-induced mechanics of membranes [8-36] among many others and studying the entropic factors in biological phenomena have now become the cornerstone of cell mechanics research. These aforementioned biophysical phenomena are governed by a complex interplay between the various attractive and repulsive forces that mediate between biological structures. A key role is played by a repulsive force termed entropic pressure, the origins of which lie in the thermally excited fluctuations of membranes. A recent topic of growing interest is the entropic interactions of nanomaterials with biological membranes with applications to nanotoxicity, cancer treatments, and drug delivery [37, 38]. Due to their excellent physical and mechanical properties, flexible nanostructures have found applications as biosensors and drug carriers [39-41]. However, there is still a lack of fundamental understanding on how an ultra-thin sheet interacts with cell membranes. It has been experimentally observed that micro-sized sheets of crystalline membranes always tend to approach a cell membrane through a sharp corner [42,44], which for hydrophobic surfaces such as graphene could lead to piercing and destructive extraction of lipid molecules [43]. A recent statistical mechanics model suggests that interactions of crystalline membranes with biological cells at the very early stage of approaching is strongly controlled by entropic factors and the resulting edge/corner approaching mode is somewhat a universal behavior of all flexible nanostructures in the vicinity of fluctuating cell membranes [45]. Some of the results are demonstrated in Figure 2 for the entropic energetic costs to bring a crystalline membrane of size 1 micrometer in distance d from a fluctuating membrane in parallel vs perpendicular approaching modes [45]. The top left picture shows a water channel created by boron nitride sheets interacting with lipid membrane [44]. The top right is a graphene oxide sheet cutting through a cell membrane with a sharp corner [42]. The bottom left shows lipid extraction of hydrophobic sheets in MD simulation [43].
Entropy-driven stability/instability of flexible nanostructures
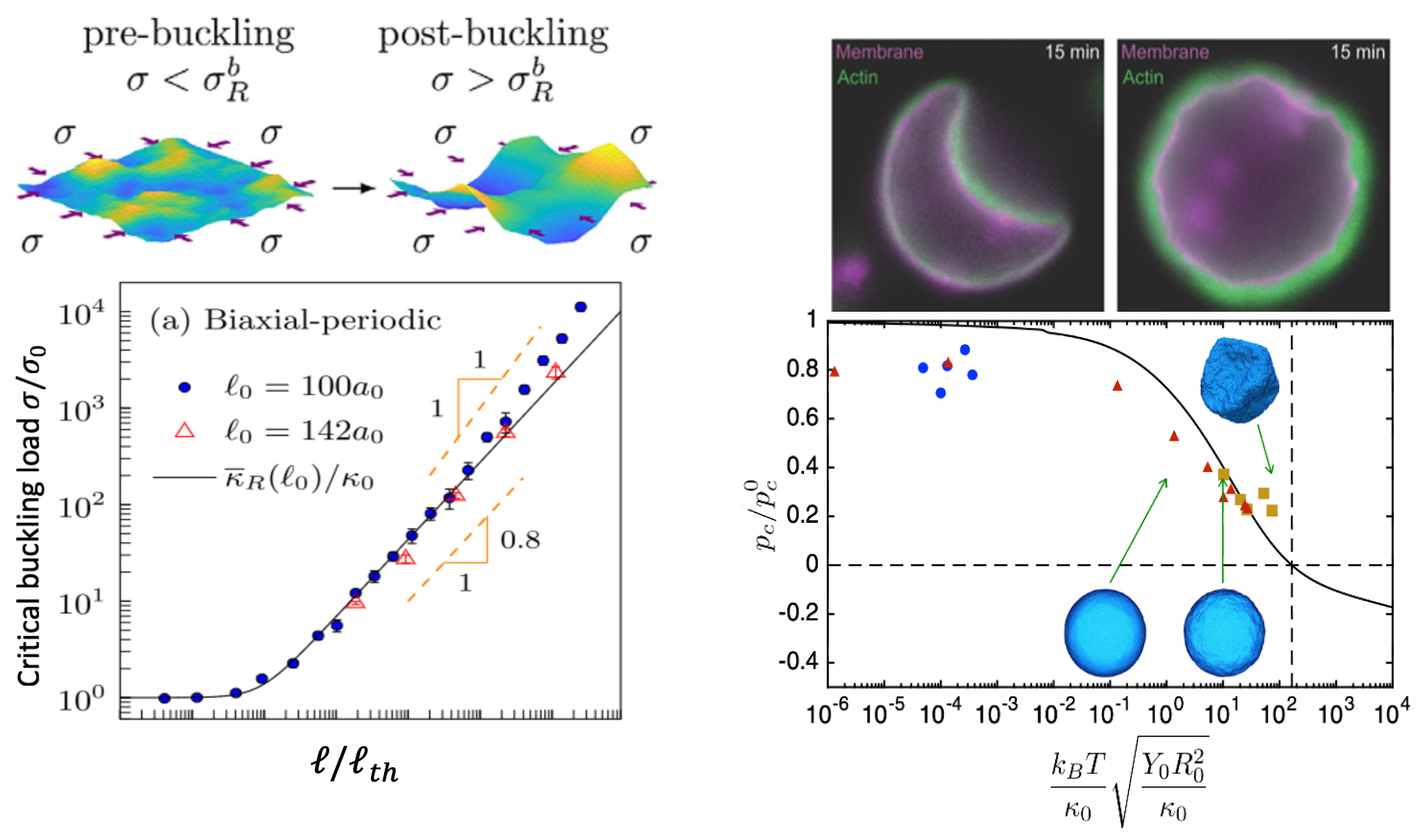
Buckling of shells and sheets at small scale recently attracted the scientific community due to their diverse set of applications ranging from pattern formation [46], structural stability of crystalline membranes [47], multifunctional kirigami nanostructures [48, 49], mechanics of colloidal capsules [50], pollen grains [51] and viruses [52]. Although for a long time, buckling has been considered as an undesirable mode of failure in structures, it is recently even intentionally introduced as a smart mechanical mechanism and plays a central role in the design of nanoscale metamaterials as they combine complex morphologies with mechanical functionality. The effect of thermal fluctuations on the buckling pathways of flat sheets and spherical shells have been extensively studied mostly in physics literature [53-57]. It is shown that thermal fluctuations increase the buckling threshold in flat sheets and decrease the critical buckling pressure for spherical shells. The results shown in Figure 3, demonstrates some quantitative results from [54, 57]. The picture in top right is an experimental picture of a buckled actin supported shell. In addition to the effect of thermal fluctuations, boundary conditions also play critical role in buckling pathways of flat sheets. For example, it has been shown that the clamped boundary condition can induce a novel thermally generated spontaneous tension and modify important scaling laws, which is typically neglected in interpreting the experimental data [53]. Figure 3 demonstrates how the critical buckling load varies with size for flat sheets [54] and spherical shells [57], at finite temperature, along with an experimental picture of a buckled actin-supported biological shell [58].
Challenges and future directions
The conventional statistical mechanics models of membranes are based on some simplifying assumptions. Here are just a few of them: 1) periodic boundary conditions in all directions to ensure translational symmetry at all points on the surface of the membrane, 2) linearization and 3) homogeneity. In real cases for both biological and crystalline membranes these simplifying assumptions are not always applicable.
For example:
- Pore formation in biological membranes is involved with an open edge. Deformation of nanoribbons of crystalline membranes is also involved with open boundaries. In such cases periodic boundary conditions cannot be applicable.
- Crystalline membranes such as graphene, boron nitride, MXene among others, are nonlinear solids. The kinematic of deformations in solid membranes are similar to that of von-Karman plate theory with nonlinear coupling of in and out-of-plane deformations. In fluid membranes such as biological membranes, large deformations may introduce geometric nonlinearities in the energy functional. Unfortunately, carrying out statistical mechanics of nonlinear systems is a daunting task to say the least; and closed-form solutions are frequently unobtainable. The equipartition theorem, that is the essential result used by nearly all the analytical statistical mechanics works on biological membranes, is not applicable.
- Biological membranes are highly heterogeneous, and the coexistence of various domains and proteins and lipid molecules is essential for cell’s viability and functionality. In large scale applications of crystalline membranes also, the effects of surface coating and atomistic defects are unavoidable that result in a nonhomogeneous surface. In such cases, the assumption of a homogeneous sheet in statistical mechanics modeling of membranes does not give us an accurate description of the mechanics of these structures. For crystalline membranes such as MXene and MoS2, the effect of anisotropy should be accounted for as well.
Most of the treatments of statistical mechanics of nonlinear sheets and tethered membranes find their origins in the developments in the high-energy physics literature [59, 60]. Accordingly, those derivations are not readily understood by the mechanics and materials science community---despite the fact that the underlying basic starting point of the statistical mechanics analysis is nonlinear elasticity and of considerable interest to those communities. Of course, no criticism is implied here. This is simply an observation that even for material scientists and mechanicians who have a reasonable understanding of statistical mechanics, Feyman's diagrams, renormalization group theory and related discipline specific etc. tend to be unfamiliar topics. Notable exceptions are recent works by Professor Freund [61] who presented a rather simple (but numerical) method based on Fourier series, and Liang and Purohit [62, 63] who used a finite element like numerical framework to discretize the membrane and then employed Gaussian integrals for the statistical mechanics. A nice advantage of the approach by Liang and Purohit [63] is the facile inclusion of boundary conditions for the fluctuations of finite membranes.
In short, developing mechanics-based statistical mechanics models of fluctuating membranes that account for nonlinearities, heterogeneities and various boundary conditions is essential for understanding the effect of thermal fluctuations on mechanical behavior and mechanically coupled properties of biological and crystalline membranes. I look forward to furthering this discussion with you in the comments section.
References
1. D. Akinwande, C. J. Brennan, J. S. Bunch, P. Egberts, J. R. Felts, H. Gao, R. Huang, J.-S. Kim, T. Li, Y. Li, et al., A review on mechanics and mechanical properties of 2d materials – graphene and beyond, Extreme Mechanics Letters (2017).
2. F. Ahmadpoor, P. Sharma, Flexoelectricity in two-dimensional crystalline and biological membranes, Nanoscale 7 (40) (2015) 16555–16570.
3. K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim, K. S. Kim, J.-H. Ahn, P. Kim, J.-Y. Choi, B. H. Hong, Large-scale pattern growth of graphene films for stretchable transparent electrodes, nature 457 (7230) (2009) 706–710.
4. K. Kostarelos, K. S. Novoselov, Exploring the interface of graphene and biology, Science 344 (6181) (2014) 261–263.
5. K. N. Kudin, G. E. Scuseria, B. I. Yakobson, C 2 f, bn, and c nanoshell elasticity from ab initio computations, Physical Review B 64 (23) (2001) 235406.
6. Q. Lu, M. Arroyo, R. Huang, Elastic bending modulus of monolayer graphene, Journal of Physics D: Applied Physics 42 (10) (2009) 102002.
7. P. Koskinen, O. O. Kit, Approximate modeling of spherical membranes, Physical Review B 82 (23) (2010) 235420.
8. Ahmadpoor, F. and Sharma, P., 2017. A perspective on the statistical mechanics of 2D materials. Extreme Mechanics Letters, 14, pp.38-43.
9. Ahmadpoor, F., Wang, P., Huang, R. and Sharma, P., 2017. Thermal fluctuations and effective bending stiffness of elastic thin sheets and graphene: A nonlinear analysis. Journal of the Mechanics and Physics of Solids, 107, pp.294-319.
10. Gao, W. and Huang, R., 2014. Thermomechanics of monolayer graphene: Rippling, thermal expansion and elasticity. Journal of the Mechanics and Physics of Solids, 66, pp.42-58.
11. Zelisko, M., Ahmadpoor, F., Gao, H. and Sharma, P., 2017. Determining the Gaussian modulus and edge properties of 2D materials: From graphene to lipid bilayers. Physical Review Letters, 119(6), p.068002.
12. Liu, L.P. and Sharma, P., 2013. Flexoelectricity and thermal fluctuations of lipid bilayer membranes: Renormalization of flexoelectric, dielectric, and elastic properties. Physical Review E, 87(3), p.032715.
13. Nelson, P. and Powers, T., 1993. Renormalization of chiral couplings in titled bilayer membranes. Journal de Physique II, 3(10), pp.1535-1569.
14. Powers, T. and Nelson, P., 1995. Fluctuating membranes with tilt order. Journal de Physique II, 5(11), pp.1671-1678.
15. Golestanian, R., Goulian, M. and Kardar, M., 1996. Fluctuation-induced interactions between rods on a membrane. Physical Review E, 54(6), p.6725.
16. Lin, H.K., Zandi, R., Mohideen, U. and Pryadko, L.P., 2011. Fluctuation-induced forces between inclusions in a fluid membrane under tension. Physical review letters, 107(22), p.228104.
17. Yolcu, C. and Deserno, M., 2012. Membrane-mediated interactions between rigid inclusions: an effective field theory. Physical Review E, 86(3), p.031906.
18. Salditt, T., 2005. Thermal fluctuations and stability of solid-supported lipid membranes. Journal of Physics: Condensed Matter, 17(6), p.R287.
19. Auth, T., Safran, S.A. and Gov, N.S., 2007. Fluctuations of coupled fluid and solid membranes with application to red blood cells. Physical Review E, 76(5), p.051910.
20. Hu, M., Briguglio, J.J. and Deserno, M., 2012. Determining the Gaussian curvature modulus of lipid membranes in simulations. Biophysical journal, 102(6), pp.1403-1410.
21. R. Lipowsky, U. Seifert, Adhesion of vesicles and membranes, Molecular crystals and liquid crystals 202 (1) (1991) 17–25.
22. R. Lipowsky, S. Leibler, Unbinding transitions of interacting membranes, Physical Review Letters 56 (23) (1986) 2541.
23. J.-H. Lee, S.-M. Choi, C. Doe, A. Faraone, P. A. Pincus, S. R. Kline, Thermal fluctuation and elasticity of lipid vesicles interacting with pore-forming peptides, Physical review letters 105 (3) (2010) 038101.
24. T. R. Weikl, R. Lipowsky, Pattern formation during t-cell adhesion, Biophysical journal 87 (6) (2004) 3665–3678.
25. W. Chen, E. A. Evans, R. P. McEver, C. Zhu, Monitoring receptor-ligand interactions between surfaces by thermal fluctuations, Biophysical journal 94 (2) (2008) 694–701.
26. H. Gao, W. Shi, L. B. Freund, Mechanics of receptor-mediated endocytosis, Proceedings of the National Academy of Sciences 102 (27) (2005) 9469–9474.
27. F. Ahmadpoor, P. Sharma, Thermal fluctuations of vesicles and nonlinear curvature elastic- ity—implications for size-dependent renormalized bending rigidity and vesicle size distribution, Soft matter 12 (9) (2016) 2523–2536.
28. N. Gov, A. Zilman, S. Safran, Cytoskeleton confinement and tension of red blood cell mem- branes, Physical review letters 90 (22) (2003) 228101.
29. M. Dearnley, T. Chu, Y. Zhang, O. Looker, C. Huang, N. Klonis, J. Yeoman, S. Kenny, M. Arora, J. M. Osborne, et al., Reversible host cell remodeling underpins deformability changes in malaria parasite sexual blood stages, Proceedings of the National Academy of Sciences 113 (17) (2016) 4800–4805.
30. L. Fisher, Force between biological surfaces, Journal of the Chemical Society, Faraday Trans- actions 89 (15) (1993) 2567–2582.
31. O. Farago, C. D. Santangelo, Pore formation in fluctuating membranes, The Journal of chemical physics 122 (4) (2005) 044901.
32. T. Auth, S. Safran, N. S. Gov, Fluctuations of coupled fluid and solid membranes with application to red blood cells, Physical Review E 76 (5) (2007) 051910.
33. W. Helfrich, Size distributions of vesicles: the role of the effective rigidity of membranes, Journal de Physique 47 (2) (1986) 321–329.
34. C. Huang, D. Quinn, Y. Sadovsky, S. Suresh, K. J. Hsia, Formation and size distribution of self-assembled vesicles, Proceedings of the National Academy of Sciences 114 (11) (2017) 2910–2915.
35. L. Freund, Entropic pressure between biomembranes in a periodic stack due to thermal fluctuations, Proceedings of the National Academy of Sciences 110 (6) (2013) 2047–2051.
36. P. Sharma, Entropic force between membranes reexamined, Proceedings of the National Academy of Sciences 110 (6) (2013) 1976–1977.
37. J. Wang, Y. Wei, X. Shi, H. Gao, Cellular entry of graphene nanosheets: the role of thickness, oxidation and surface adsorption, Rsc Advances 3 (36) (2013) 15776–15782.
38. H. Gao, Probing mechanical principles of cell–nanomaterial interactions, Journal of the Mechanics and Physics of Solids 62 (2014) 312–339.
39. T. Kuila, S. Bose, P. Khanra, A. K. Mishra, N. H. Kim, J. H. Lee, Recent advances in graphene-based biosensors, Biosensors and Bioelectronics 26 (12) (2011) 4637–4648.
40. M. Kalbacova, A. Broz, J. Kong, M. Kalbac, Graphene substrates promote adherence of human osteoblasts and mesenchymal stromal cells, Carbon 48 (15) (2010) 4323–4329.
41. T. R. Nayak, H. Andersen, V. S. Makam, C. Khaw, S. Bae, X. Xu, P.-L. R. Ee, J.-H. Ahn, B. H. Hong, G. Pastorin, Graphene for controlled and accelerated osteogenic differentiation of human mesenchymal stem cells, ACS nano 5 (6) (2011) 4670–4678.
42. Li, Y., Yuan, H., von Dem Bussche, A., Creighton, M., Hurt, R.H., Kane, A.B. and Gao, H., 2013. Graphene microsheets enter cells through spontaneous membrane penetration at edge asperities and corner sites. Proceedings of the National Academy of Sciences, 110(30), pp.12295-12300.
43. Tu, Y., Lv, M., Xiu, P., Huynh, T., Zhang, M., Castelli, M., Liu, Z., Huang, Q., Fan, C., Fang, H. and Zhou, R., 2013. Destructive extraction of phospholipids from Escherichia coli membranes by graphene nanosheets. Nature nanotechnology, 8(8), pp.594-601.
44. M. A. Lucherelli, X. Qian, P. Weston, M. Eredia, W. Zhu, P. Samor`ı, H. Gao, A. Bianco, A. von dem Bussche, Boron nitride nanosheets can induce water channels across lipid bilayers leading to lysosomal permeabilization, Advanced Materials 33 (45) (2021) 2103137.
45. Ahmadpoor, F., Zou, G. and Gao, H., 2022. Entropic interactions of 2D materials with cellular membranes: Parallel versus perpendicular approaching modes. Mechanics of Materials, 174, p.104414.
46. J. Yin, Z. Cao, C. Li, I. Sheinman, X. Chen, Stress-driven buckling patterns in spheroidal core/shell structures, Proceedings of the National Academy of Sciences 105 (49) (2008) 19132– 19135.
47. A. V. Thomas, B. C. Andow, S. Suresh, O. Eksik, J. Yin, A. H. Dyson, N. Koratkar, Con- trolled crumpling of graphene oxide films for tunable optical transmittance, Advanced mate- rials 27 (21) (2015) 3256–3265.
48. M. K. Blees, A. W. Barnard, P. A. Rose, S. P. Roberts, K. L. McGill, P. Y. Huang, A. R. Ruyack, J. W. Kevek, B. Kobrin, D. A. Muller, et al., Graphene kirigami, Nature 524 (7564) (2015) 204–207.
49. C. Dai, Y. Rho, K. Pham, B. McCormick, B. W. Blankenship, W. Zhao, Z. Zhang, S. M. Gilbert, M. F. Crommie, F. Wang, et al., Kirigami engineering of suspended graphene trans- ducers, Nano Letters (2022).
50. S. S. Datta, S.-H. Kim, J. Paulose, A. Abbaspourrad, D. R. Nelson, D. A. Weitz, Delayed buckling and guided folding of inhomogeneous capsules, Physical review letters 109 (13) (2012) 134302.
51. E. Katifori, S. Alben, E. Cerda, D. R. Nelson, J. Dumais, Foldable structures and the natural design of pollen grains, Proceedings of the National Academy of Sciences 107 (17) (2010) 7635–7639.
52. J. Lidmar, L. Mirny, D. R. Nelson, Virus shapes and buckling transitions in spherical shells, Physical Review E 68 (5) (2003) 051910.
53. S. Shankar, D. R. Nelson, Thermalized buckling of isotropically compressed thin sheets, Physical Review E 104 (5) (2021) 054141.
54. Morshedifard, A., Ruiz-García, M., Qomi, M.J.A. and Košmrlj, A., 2021. Buckling of thermalized elastic sheets. Journal of the Mechanics and Physics of Solids, 149, p.104296.
55. Hanakata, P.Z., Bhabesh, S.S., Bowick, M.J., Nelson, D.R. and Yllanes, D., 2021. Thermal buckling and symmetry breaking in thin ribbons under compression. Extreme Mechanics Letters, 44, p.101270.
56. Paulose, J., Vliegenthart, G.A., Gompper, G. and Nelson, D.R., 2012. Fluctuating shells under pressure. Proceedings of the National Academy of Sciences, 109(48), pp.19551-19556.
57. Košmrlj, A. and Nelson, D.R., 2017. Statistical mechanics of thin spherical shells. Physical Review X, 7(1), p.011002.
58. R. Kusters, C. Simon, R. L. Dos Santos, V. Caorsi, S. Wu, J.-F. Joanny, P. Sens, C. Sykes, Actin shells control buckling and wrinkling of biomembranes, Soft Matter 15 (47) (2019) 9647–9653.
59. Goldenfeld, N., 2018. Lectures on phase transitions and the renormalization group. CRC Press.
60. Amit, D.J. and Martin-Mayor, V., 2005. Field theory, the renormalization group, and critical phenomena: graphs to computers. World Scientific Publishing Company.
61. Freund, L., 2013. Entropic pressure between biomembranes in a periodic stack due to thermal fluctuations. Proc. Natl. Acad. Sci. 110 (6), 2047–2051.
62. Liang, X., Purohit, P.K., 2016. A fluctuating elastic plate and a cell model for lipid membranes. J. Mech. Phys. Solids 90, 29–44.
63. Liang, X., Purohit, P.K., 2016. A fluctuating elastic plate model applied to graphene. J. Appl. Mech. 83 (8), 081008.
| Attachment | Size |
|---|---|
| 1.05 MB | |
| 309.27 KB | |
| 1.2 MB |
- Fatemeh Ahmadpoor's blog
- Log in or register to post comments
- 10696 reads


Comments
Dear Fatemeh,
Dear Fatemeh,
Thanks for leading the discussion on this interesting topic! I got interested in the thermal rippling of graphene during my PhD work about 10 years ago. Along with Prof. Rui Huang, we studied the thermal rippling with statistical mechanics and molecular dynamics simulation and found considerable entropic contribution to the thermomechanical behavior of graphene due to the rippling [10]. Harmonic approximation was applied in our analysis, and we found the difference between the theory and MD because of the anharmonic coupling between bending and stretching modes. I'm very impressed by your later work [9] in which the anharmonic effect was included in the analysis to the first order approximation. Can you provide some comments on how this anharmonic effect plays important role in biological system? Thanks!
Wei
Hello Wei,
Hello Wei,
Thanks for your interest in this post. Yes, in fact your 2014 paper on thermomechanics of graphene [10] was our motivation to develop a statistical mechanics model that includes the nonlinear elasticity of crystalline membranes [9].
About the application of nonlinear statistical mechanics model for biological membranes, there are several cases where the linearized version of Helfrich energy does not give us a reliable model of the mechanics of biomembranes. Here I am only pointing to two of them as examples:
1) Biological vesicles are curved surfaces and deformation of the membrane is coupled with the pre-exisiting curvature field on the membrane. As a result, the mean curvature of the deformed surface will be highly nonlinear in terms of the out-of-plane displacement field. In addition to the geometric nonlinearity, the elasticity of membranes could be constitutively nonlinear as well. The constitutive nonlinearity is typically small and neglected in classical continuum mechanics models, but can result in remarkable entropic effects. One example is the size distribution of the vesicles that we studied in [27].
2) The elasticity of red blood cells membranes is typically studied using a coupled solid-fluid (polymerized) membrane system, where the interaction of phospholipid membrane with the underlying skeleton leads to a shear resistance [R1]. The kinematic of the deformation in this case is best described within nonlinear von-Karman plate theory... much like graphene and other crystalline membranes. Such nonlinearity is suggested to describe the mechanics of viral capsid [R2] and actin-supported biological shells as well [58].
R1: Discher, D.E., Boal, D.H. and Boey, S.K., 1998. Simulations of the erythrocyte cytoskeleton at large deformation. II. Micropipette aspiration. Biophysical Journal, 75(3), pp.1584-1597.
R2: May, E.R. and Brooks III, C.L., 2011. Determination of viral capsid elastic properties from equilibrium thermal fluctuations. Physical review letters, 106(18), p.188101.
statistical mechanics of membranes
Dear Fatemeh,
Thank you for the stimulating and timely article on the topic of statistical mechanics of membranes. Indeed, combining tools from equilibrium statistical mechanics with continuum mechanics models can furnish valuable insights into many interesting problems in biology and materials science. You have provided excellent examples of biological phenomena and processes where thermal fluctuations are known to play a vital role. I have two questions in the context of biological membranes.
1. It is known that surface tension can significantly impact the thermal fluctuations of membranes. That is, a tensionless membrane shows larger fluctuations than a tense membrane. Yet, surface tension is often neglected in many studies based on statistical mechanics of biological membranes. I was curious if you or other researchers have looked into estimating the contribution from surface tension in some of the phenomena where thermal fluctuations are important, such as entropy-driven instabilities or vesicle size distributions.
2. Most studies on biological membranes focus on modeling their equilibrium thermal fluctuations. However, in many phenomena such as pore formation or membrane fusion, the membrane may be driven away from equilibrium by non-thermal or 'active' forces which would require us to go beyond equilibrium statistical mechanics. Using tools from non-equilibrium statistical mechanics to understand some of the biophysics problems that you have mentioned would be a rich area of study. I was wondering if you could share your thoughts on this.
Dear Yashashree,
Dear Yashashree,
Thank for your interest in this discussion and raising very important questions...
Surface tension of biological membranes has been introduced in biophysics and cell mechanics literature through three totally different concepts: 1) a Lagrange multiplier to ensure the area is fixed under deformation, 2) simply a mechanical stiffness for producing in-plane stretch (in this case area is not necessarily fixed.), 3) Entropic tension, which is the derivative of the total free energy (as opposed to the ground state elastic energy) with respect to the area. The technical descriptions of these types of surface tension are also different, but yes, they all result in a reduction in thermal fluctuatuions. In pure lipid membranes, the entropic characteristics of a tension less membrane is expected to be stronger than that of a tense membrane. Real cell membranes are however, heterogeneous structures due to the presence of various proteins and domains and the interplay between these components are regulated by membrane surface tension. One example is the role of entropic surface tension on the gating of the mechanosensitive ion channels [R1]. In short, although the presence of surface tension reduce the fluctuations of the membrane, the resulting entropic effects in real biological cases are not always trivial and demand extensive continuum and statistical mechanics research.
I cannot agree with you more on the nessecitiy of accounting for nonequilibrium entropic effects, particularly in cell mechanics research. Currenlty, the majority of studies on cell mechanics are focused on using continuum mechanics modeling to understand the role of these active forces on biological phenomena. On the other hand, the study of entropic effects are limitted to equilibrium cases where there is no active force. Indeed, these two aspects should be studied within a unified continnum and nonequilibrium statistical mechanics framework to provide us with a comprehensive knowledge of the mechanics and physics of biological systems.
R1: Lindén, Martin, Pierre Sens, and Rob Phillips. "Entropic tension in crowded membranes." PLoS computational biology8.3 (2012): e1002431.