You are here
Journal Club for June 2018: Modeling dislocation mediated plasticity using meso-scale discrete dislocation dynamics
Ill Ryu
Department of Mechanical Engineering
The Erik Jonsson School of Engineering & Computer Science
UT Dallas
1. Introduction
The urgent challenges and opportunities for the development of future technology is significantly accelerating advances in materials research. Among these efforts, nanostructured materials are increasingly attracting attention, due to not only their improved properties in strength, toughness, and thermal stability, but also their potential to save energy by reducing the weight of structural systems.
For more than a decade, remarkable scientific progress has been achieved via a powerful collection of simulation and modeling of materials at various temporal and spatial scales. Taking advantage of this key opportunity requires underpinning material behaviors at the mesoscale. It is at this at this scale that the properties of materials and chemical reactions are determined. Based on the recently developed and still-investigated knowledge at the fundamental atomic length scale, mesoscale research will provide emerging capabilities in predictive modeling and simulation that have the potential to revolutionize the development of new materials [1, 2].
In this journal club, we would like to discuss recent understanding and latest modeling efforts, especially using discrete dislocation dynamics (DDD) modeling. We will skip the basic concepts on DDD, which can be found in several books [3-6] and excellent review papers [7-9] published in journals. Afterwards, I would like to bring up some challenges in the field.
2. Current understanding on dislocation mediated plasticity
The fundamental mechanism of plastic deformation is a shear process by the dislocation motion, as shown in Figure 1. By exploring the detailed dynamic motion of dislocations, we can predict the mechanical behavior emerging from the collective behavior of dislocations directly from the microscale. Here are few recent findings on dislocation-mediated plasticity at mesoscale.
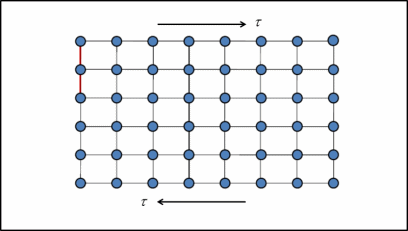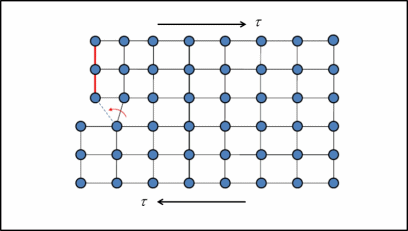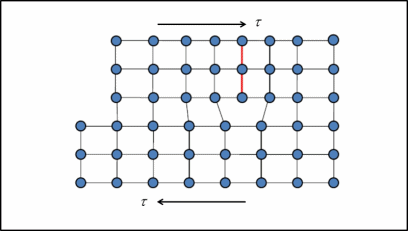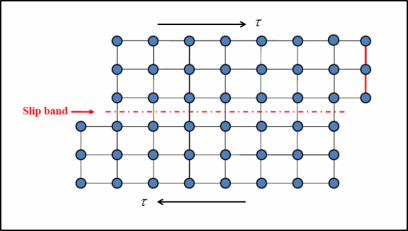
Figure 1. Plastic deformation as a slip process[10]
2-1. Understanding deformation mechanisms from dislocation sources
From many recent micromechanical experiments, 'smaller is stronger' phenomena are now well-documented [11-13] in small structures. Among proposed models for the size dependent plasticity in FCC metals, commonly accepted explanations are the dislocation starvation (DS) model [14, 15] and the single arm source (SAS) model [16-21]. According to the DS model, smaller samples contain fewer dislocation sources making it easier for dislocations to escape and requiring higher stresses to generate new dislocations for sustained plastic deformation. In the SAS model, the lengths of the truncated sources are shorter in smaller samples, so that higher stresses are required to operate them. The DDD model with surface nucleation scheme can capture the source-driven plasticity mechanisms in FCC micropillars, as shown in Figure 2.
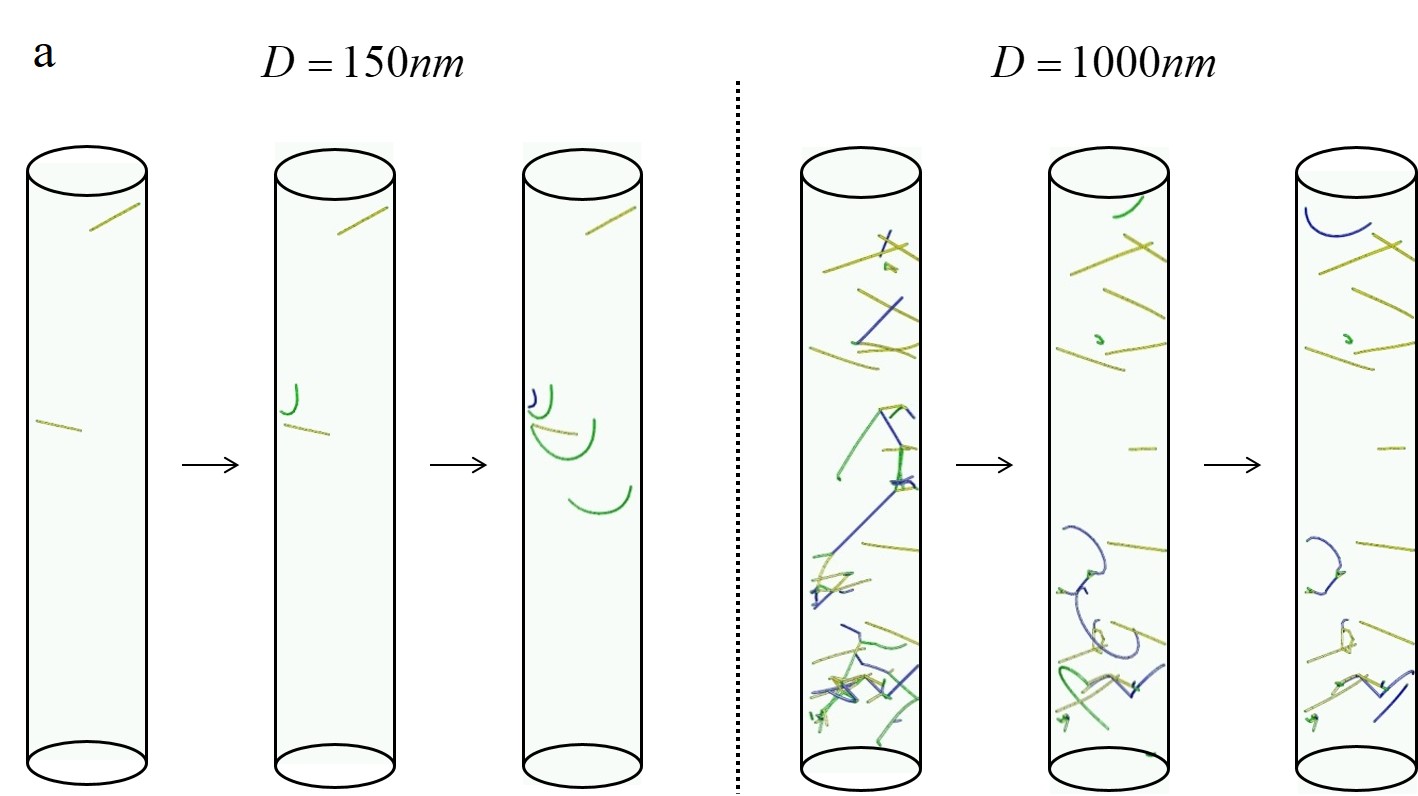
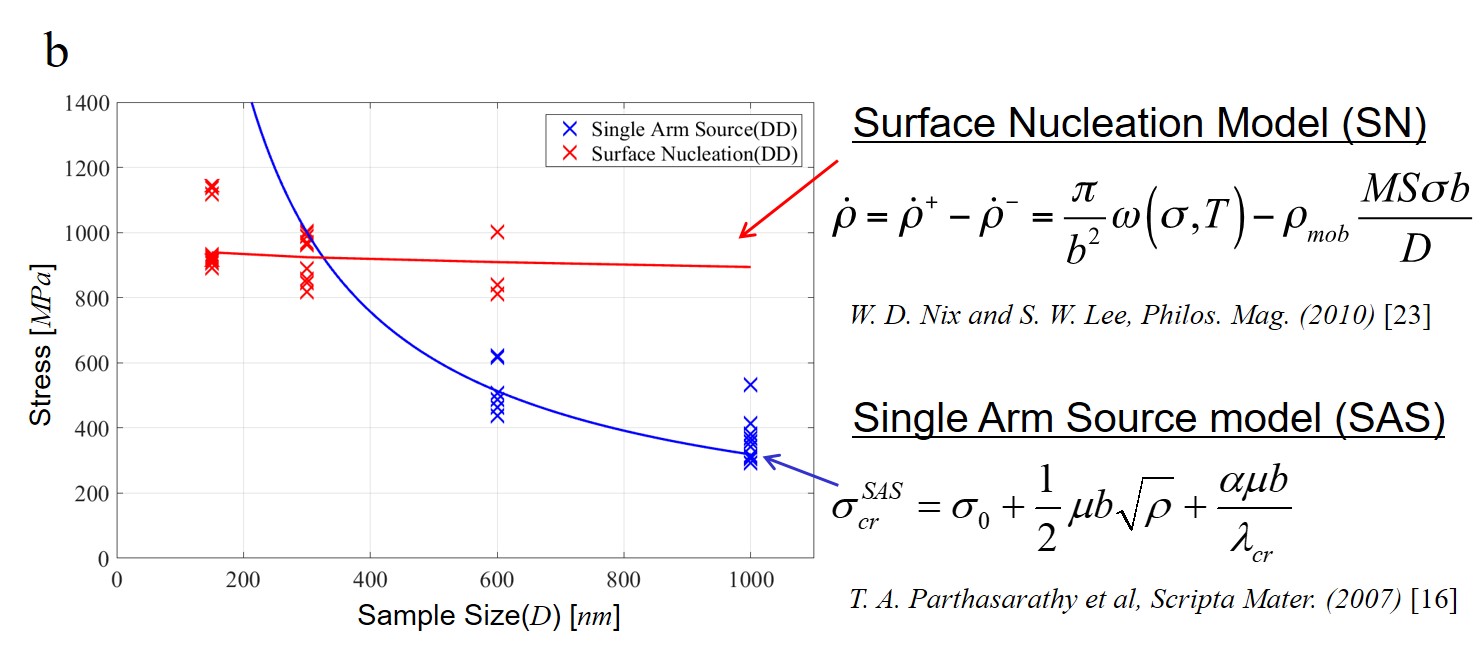
Figure 2. (a)Dislocation microstructure in FCC micropillars with the diameter of 150 nm(left) and 1000 nm(right). It can be seen that there is surface nucleation in the 150nm sample, and single arm operation in the 1000nm sample. (b) Comparison between DD results and theoretical models of SAS and SN Mechanisms [16, 22, 23].
In BCC metals, dislocation plasticity is thought to be governed mainly by the motion of screw dislocations, which have a low mobility, attributed to a non-planar core structure and a high Peierls barrier [24, 25]. In addition, from molecular dynamics (MD) simulations, dislocation multiplication is expected to occur by a process of surface induced cross-slip, while isolated screw dislocations, aided by image stresses, can self-multiply and generate sources of dislocations [26].With modified dislocation mobility, the size dependent plasticity could be also explained in DDD modeling, as shown in Figure 3.

Figure 3. Dislocation microstructure in BCC micropillars with the diameter of 150 nm(left) and 1000 nm(right).
2-2. Loading mechanism dependent dislocation microstructures and corresponding mechanical behaviors
Compared with their bulk counterparts, micron- and submicron-scale metallic samples have shown elevated flow stresses in various loading conditions, including micropillar compression/tension [14, 15, 27-34], wire torsion [35-38], foil bending [39-41] and micro- and nano-indentation [42-44]. Since conventional continuum theories are unable to capture the observed size effect, it is important to investigate detailed dislocation microstructures under various loading conditions and their corresponding mechanical response. As shown in Figure 4 below, different loading conditions gives rise to quite different microstructures at the small scale. Based on this observation it could limit the continuum approach where mechanical behaviors are mainly characterized by simple tension experiments.
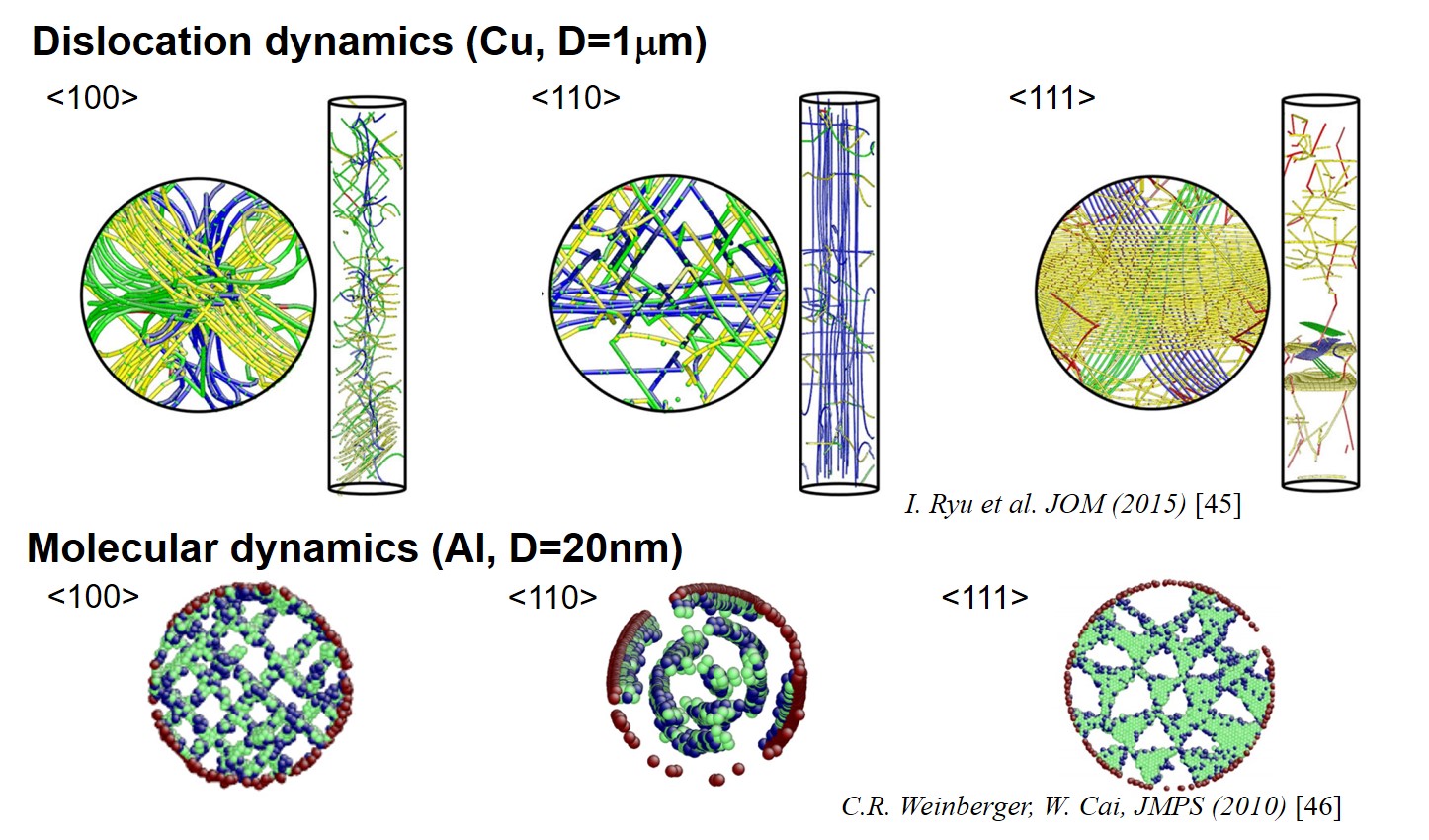
Figure 4. Dislocation microstructure in FCC micropillars and torsion in DDD model[45] and MD model [46].
3. Challenges & perspectives
3-1. Effects of vacancies/impurities and their interaction with dislocations
Based on the detailed knowledge gathered from indirect experiments and atomistic models, the mesoscale dislocation dynamics (DD) model can provide unique opportunities to study how mechanical properties change with respect to crystalline line defects. However, it is still unclear whether dislocations interact with vacancies/impurities, following general rules. This research can contribute to the fundamental knowledge of mechanical properties in the context of various types of defects.
3-2. Dislocation interaction with internal grain boundaries.
Interest in the mechanical properties of nanocrystalline metals centers on the role of grain and twin boundaries in the mechanisms of deformation. In general, GBs can either obstruct the motion of dislocations and lead to hardening [47] or they can serve as readily available sources for dislocations when plasticity is dislocation source-limited [48]. Although some attempts have been made to investigate the role of impenetrable GBs in mechanical behaviors of crystalline materials [49-52], there is still lack of models to follow general rules[53-55], specifying the various interaction modes between dislocations and internal boundaries, such as penetration, absorption, desorption [56], as shown in Figure 5.
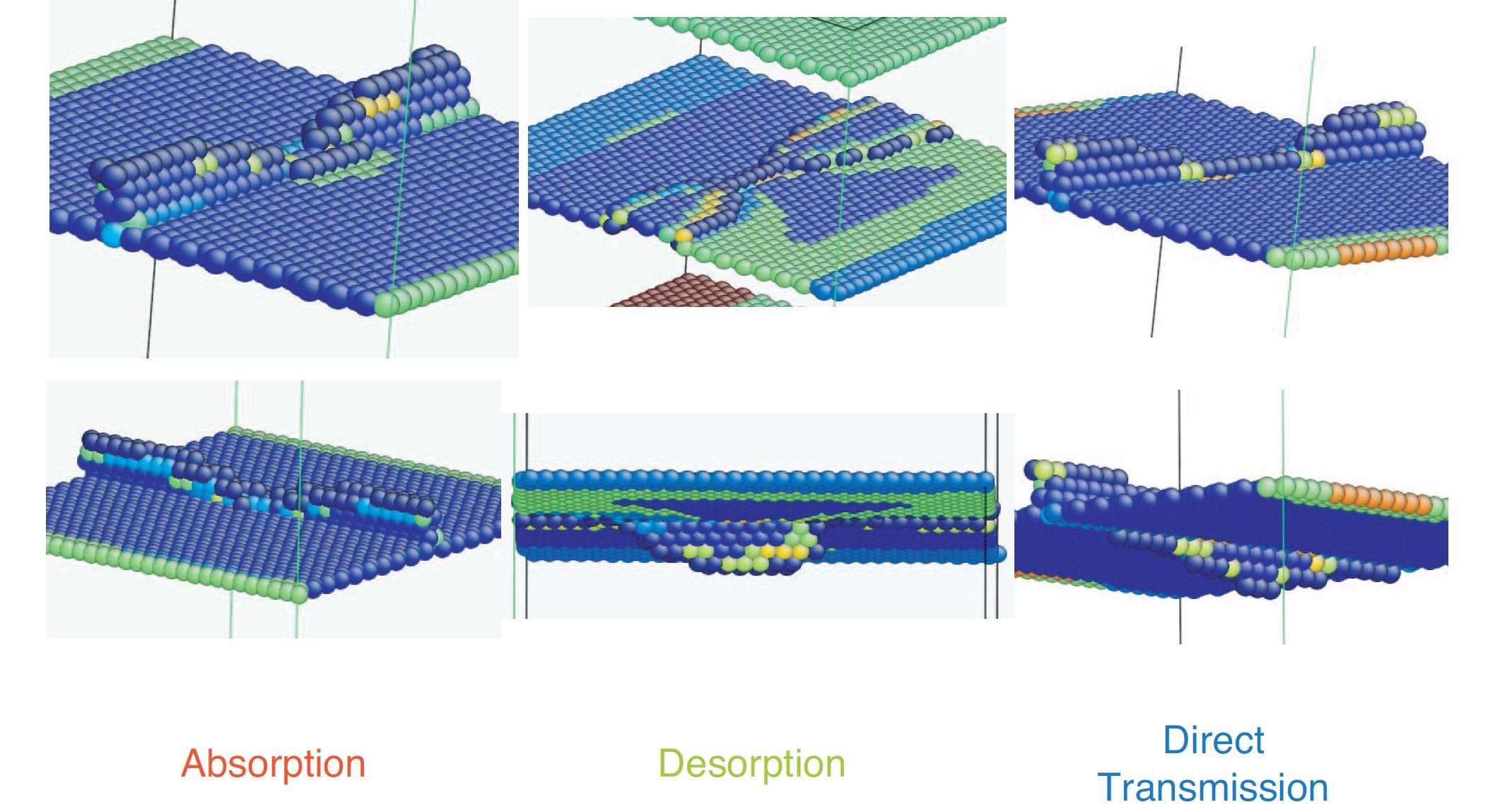
Figure 5. Atomistic modeling of interface-mediated slip transfer reactions across a twin boundary. Atomic configurations of (a) absorption, (b) desorption, and (c) direct transmission [56].
3-3. Unified multi-scale model with discrete description of dislocation motion.
The unified computational models which directly couples discrete dislocation dynamics and continuum finite element method have been developed by several groups to investigate the plastic behaviors at these scales[57-59]. These models can take advantage of both DDD and FE models; dynamic motions of dislocations are considered in DDD framework, while FEM is used to handle complex boundary and loading conditions and is also used to account for long-range dislocation interactions in an efficient way, as shown in Figure 6.
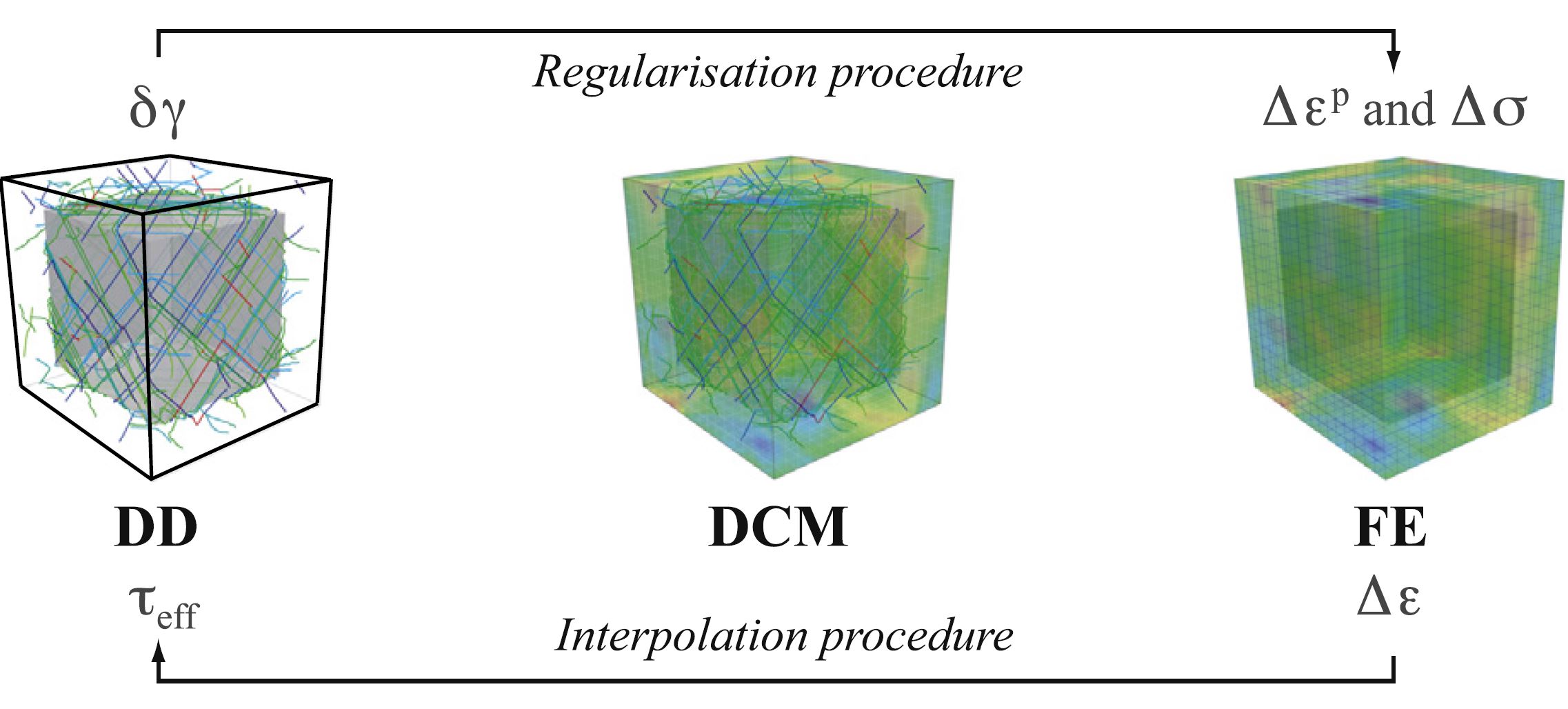
Figure 6. The schematics of coupling between DD and FE [57].
For future research, it will be necessary to develop a general model to describe the dislocation interactions with various type of defects such as impurities, grain and twin boundaries, and cracks, which will enhance our capability to predict mechanical properties of polycrystalline solids.
4. References
[1] From Quanta to the Continuum: Opportunities for Mesoscale Science, The Mesoscale Science Report (2012).
[2] G.W. Crabtree, J.L. Sarrao, Opportunities for Mesoscale Science, MRS Bulletin 37(11) (2012) 1079-1088.
[3] V.V. Bulatov, W. Cai, Computer simulations of dislocations, Oxford University Press, Oxford, 2013.
[4] L. Kubin, Dislocations, mesoscale simulations and plastic flow. http://public.eblib.com/choice/publicfullrecord.aspx?p=3055181, 2013).
[5] Z. H.M., Introduction to Discrete Dislocation Dynamics, in: S.S. Sansour C. (Ed.), Generalized Continua and Dislocation Theory, CISM Courses and Lectures,, Springer, Vienna2012.
[6] K.W.P. Sills R.B., Aghaei A., Cai W., Fundamentals of Dislocation Dynamics Simulations, in: T.G. Weinberger C. (Ed.), Multiscale Materials Modeling for Nanomechanics.Springer Series in Materials Science Springer, Cham2016, pp. 53-87.
[7] R.S. Fertig, S.P. Baker, Simulation of dislocations and strength in thin films: A review, Prog Mater Sci 54(6) (2009) 874-908.
[8] C. Zhou, S.B. Biner, R. LeSar, Discrete dislocation dynamics simulations of plasticity at small scales, Acta Mater 58(5) (2010) 1565-1577.
[9] D. Weygand, M. Mrovec, T. Hochrainer, P. Gumbsch, Multiscale Simulation of Plasticity in bcc Metals, Annual Review of Materials Research 45(1) (2015) 369-390.
[10] W. Cai, W.D. Nix, S. Materials Research, Imperfections in crystalline solids, 2016.
[11] J.R. Greer, J.T.M. De Hosson, Plasticity in small-sized metallic systems: Intrinsic versus extrinsic size effect, Prog Mater Sci 56(6) (2011) 654-724.
[12] O. Kraft, P.A. Gruber, R. Monig, D. Weygand, Plasticity in Confined Dimensions, Annu Rev Mater Res 40 (2010) 293-317.
[13] M.D. Uchic, P.A. Shade, D.M. Dimiduk, Plasticity of Micrometer-Scale Single Crystals in Compression, Annual Review of Materials Research 39 (2009) 361-386.
[14] J.R. Greer, W.D. Nix, Nanoscale gold pillars strengthened through dislocation starvation, Phys Rev B 73(24) (2006).
[15] W.D. Nix, J.R. Greer, G. Feng, E.T. Lilleodden, Deformation at the nanometer and micrometer length scales: Effects of strain gradients and dislocation starvation, Thin Solid Films 515(6) (2007) 3152-3157.
[16] T.A. Parthasarathy, S.I. Rao, D.M. Dimiduk, M.D. Uchic, D.R. Trinkle, Contribution to size effect of yield strength from the stochastics of dislocation source lengths in finite samples, Scripta Mater 56(4) (2007) 313-316.
[17] S.I. Rao, D.M. Dimiduk, T.A. Parthasarathy, M.D. Uchic, M. Tang, C. Woodward, Athermal mechanisms of size-dependent crystal flow gleaned from three-dimensional discrete dislocation simulations, Acta Mater 56(13) (2008) 3245-3259.
[18] S.I. Rao, D.M. Dimiduk, M. Tang, T.A. Parthasarathy, M.D. Uchic, C. Woodward, Estimating the strength of single-ended dislocation sources in micron-sized single crystals, Philos Mag 87(30) (2007) 4777-4794.
[19] K.S. Ng, A.H.W. Ngan, Breakdown of Schmid's law in micropillars, Scripta Mater 59(7) (2008) 796-799.
[20] J.A. El-Awady, M. Wen, N.M. Ghoniem, The role of the weakest-link mechanism in controlling the plasticity of micropillars, J Mech Phys Solids 57(1) (2009) 32-50.
[21] F. Mompiou, M. Legros, A. Sedlmayr, D.S. Gianola, D. Caillard, O. Kraft, Source-based strengthening of sub-micrometer Al fibers, Acta Mater 60(3) (2012) 977-983.
[22] I. Ryu, W. Cai, W.D. Nix, H.J. Gao, Stochastic behaviors in plastic deformation of face-centered cubic micropillars governed by surface nucleation and truncated source operation, Acta Mater 95 (2015) 176-183.
[23] W.D. Nix, S.-W. Lee, Micro-pillar plasticity controlled by dislocation nucleation at surfaces, Philos Mag 91(7-9) (2011) 1084-1096.
[24] W. Cai, V.V. Bulatov, Mobility laws in dislocation dynamics simulations, Materials Science and Engineering: A 387-389 (2004) 277-281.
[25] G. Po, Y. Cui, D. Rivera, D. Cereceda, T.D. Swinburne, J. Marian, N. Ghoniem, A phenomenological dislocation mobility law for bcc metals, Acta Mater 119 (2016) 123-135.
[26] C.R. Weinberger, W. Cai, Surface-controlled dislocation multiplication in metal micropillars, Proceedings of the National Academy of Sciences 105(38) (2008) 14304-14307.
[27] J.R. Greer, W.C. Oliver, W.D. Nix, Size dependence of mechanical properties of gold at the micron scale in the absence of strain gradients, Acta Mater 53(6) (2005) 1821-1830.
[28] M.D. Uchic, D.M. Dimiduk, J.N. Florando, W.D. Nix, Sample dimensions influence strength and crystal plasticity, Science 305(5686) (2004) 986-989.
[29] D. Kiener, W. Grosinger, G. Dehm, R. Pippan, A further step towards an understanding of size-dependent crystal plasticity: In situ tension experiments of miniaturized single-crystal copper samples, Acta Mater 56(3) (2008) 580-592.
[30] K.S. Ng, A.H.W. Ngan, Stochastic nature of plasticity of aluminum micro-pillars, Acta Mater 56(8) (2008) 1712-1720.
[31] D.M. Dimiduk, M.D. Uchic, T.A. Parthasarathy, Size-affected single-slip behavior of pure nickel microcrystals, Acta Mater 53(15) (2005) 4065-4077.
[32] D.M. Dimiduk, C. Woodward, R. LeSar, M.D. Uchic, Scale-free intermittent flow in crystal plasticity, Science 312(5777) (2006) 1188-1190.
[33] C.A. Volkert, E.T. Lilleodden, Size effects in the deformation of sub-micron Au columns, Philos Mag 86(33-35) (2006) 5567-5579.
[34] D. Kiener, C. Motz, T. Schoberl, M. Jenko, G. Dehm, Determination of mechanical properties of copper at the micron scale, Adv Eng Mater 8(11) (2006) 1119-1125.
[35] N.A. Fleck, G.M. Muller, M.F. Ashby, J.W. Hutchinson, Strain Gradient Plasticity - Theory and Experiment, Acta Metall Mater 42(2) (1994) 475-487.
[36] D.J. Dunstan, B. Ehrler, R. Bossis, S. Joly, K.M.Y. P'ng, A.J. Bushby, Elastic Limit and Strain Hardening of Thin Wires in Torsion, Phys Rev Lett 103(15) (2009).
[37] D.B. Liu, Y.M. He, D.J. Dunstan, B. Zhang, Z.P. Gan, P. Hu, H.M. Ding, Toward a further understanding of size effects in the torsion of thin metal wires: An experimental and theoretical assessment, Int J Plasticity 41 (2013) 30-52.
[38] D.B. Liu, Y.M. He, D.J. Dunstan, B. Zhang, Z.P. Gan, P. Hu, H.M. Ding, Anomalous Plasticity in the Cyclic Torsion of Micron Scale Metallic Wires, Phys Rev Lett 110(24) (2013).
[39] J.S. Stolken, A.G. Evans, A microbend test method for measuring the plasticity length scale, Acta Mater 46(14) (1998) 5109-5115.
[40] M.A. Haque, M.T.A. Saif, Strain gradient effect in nanoscale thin films, Acta Mater 51(11) (2003) 3053-3061.
[41] C. Motz, D. Weygand, J. Senger, P. Gumbsch, Micro-bending tests: A comparison between three-dimensional discrete dislocation dynamics simulations and experiments, Acta Mater 56(9) (2008) 1942-1955.
[42] Q. Ma, D.R. Clarke, Size-Dependent Hardness of Silver Single-Crystals, J Mater Res 10(4) (1995) 853-863.
[43] W.D. Nix, Mechanical-Properties of Thin-Films, Metall Trans A 20(11) (1989) 2217-2245.
[44] N.A. Stelmashenko, M.G. Walls, L.M. Brown, Y.V. Milman, Microindentations on W and Mo Oriented Single-Crystals - an Stm Study, Acta Metall Mater 41(10) (1993) 2855-2865.
[45] I. Ryu, W. Cai, W.D. Nix, H.J. Gao, Anisotropic Size-Dependent Plasticity in Face-Centered Cubic Micropillars Under Torsion, Jom-Us 68(1) (2016) 253-260.
[46] C.R. Weinberger, W. Cai, Orientation-Dependent Plasticity in Metal Nanowires under Torsion: Twist Boundary Formation and Eshelby Twist, Nano Lett 10(1) (2010) 139-142.
[47] B. Yang, H. Vehoff, Dependence of nanohardness upon indentation size and grain size - A local examination of the interaction between dislocations and grain boundaries, Acta Mater 55(3) (2007) 849-856.
[48] E.T. Lilleodden, W.D. Nix, Microstructural length-scale effects in the nanoindentation behavior of thin gold films, Acta Mater 54(6) (2006) 1583-1593.
[49] H.D. Fan, S. Aubry, A. Arsenlis, J.A. El-Awady, The role of twinning deformation on the hardening response of polycrystalline magnesium from discrete dislocation dynamics simulations, Acta Mater 92 (2015) 126-139.
[50] H.D. Fan, S. Aubry, A. Arsenlis, J.A. El-Awady, Orientation influence on grain size effects in ultrafine-grained magnesium, Scripta Mater 97 (2015) 25-28.
[51] H.D. Fan, Z.H. Li, M.S. Huang, Toward a further understanding of intermittent plastic responses in the compressed single/bicrystalline micropillars, Scripta Mater 66(10) (2012) 813-816.
[52] D.S. Balint, V.S. Deshpande, A. Needleman, E. Van der Giessen, Discrete dislocation plasticity analysis of the grain size dependence of the flow strength of polycrystals, Int J Plasticity 24(12) (2008) 2149-2172.
[53] J. Kacher, B.P. Eftink, B. Cui, I.M. Robertson, Dislocation interactions with grain boundaries, Current Opinion in Solid State and Materials Science 18(4) (2014) 227-243.
[54] T.R. Bieler, P. Eisenlohr, C. Zhang, H.J. Phukan, M.A. Crimp, Grain boundaries and interfaces in slip transfer, Current Opinion in Solid State and Materials Science 18(4) (2014) 212-226.
[55] D.E. Spearot, M.D. Sangid, Insights on slip transmission at grain boundaries from atomistic simulations, Current Opinion in Solid State and Materials Science 18(4) (2014) 188-195.
[56] T. Zhu, J. Li, A. Samanta, H.G. Kim, S. Suresh, Interfacial plasticity governs strain rate sensitivity and ductility in nanostructured metals, P Natl Acad Sci USA 104(9) (2007) 3031-3036.
[57] A. Vattré, B. Devincre, F. Feyel, R. Gatti, S. Groh, O. Jamond, A. Roos, Modelling crystal plasticity by 3D dislocation dynamics and the finite element method: The Discrete-Continuous Model revisited, J Mech Phys Solids 63 (2014) 491-505.
[58] Z.L. Liu, X.M. Liu, Z. Zhuang, X.C. You, A multi-scale computational model of crystal plasticity at submicron-to-nanometer scales, Int J Plasticity 25(8) (2009) 1436-1455.
[59] A. Vattré, B. Devincre, A. Roos, Orientation dependence of plastic deformation in nickel-based single crystal superalloys: Discrete–continuous model simulations, Acta Mater 58(6) (2010) 1938-1951.
| Attachment | Size |
|---|---|
| 116.97 KB | |
| 103.14 KB | |
| 132.2 KB | |
| 189.36 KB | |
| 270.96 KB | |
| 276.26 KB | |
| 182.69 KB |
- ill.ryu's blog
- Log in or register to post comments
- 25237 reads



Comments
I look forward to hearing your thoughts
I look forward to hearing your questions and comments.
Modeling boundaries
Dear Ill,
Thank you for an insightful overview of mesoscale plasticity modeling. As you pointed out, one of the outstanding challenges is modeling dislocation-interface interaction. What are the barriers toward developing a set of rules for such interactions? Does stochasticity have a role to play? Are there efforts in the concurrent modeling approach to model interfacial regions using atomistic discretization while the bulk regions may be modeled using DD/ homogenized continua?
Thanks,
Shailendra
Re: Modeling boundaries
To answer your first question regarding difficulty in developing a set of rules for such interactions, it mainly results from the fact that there are many parameters to characterize grain boundaries and dislocations. Specifically, the geometry of a grain boundary can be characterized by 5 degrees of freedom (dof): 3 for the relative misorientation between the two grains, and 2 for the direction of the grain boundary plane normal. Likewise, it also require 5 dof for dislocations: 3 Burgers vector and 2 for the direction. In addition, intrinsic material properties would be also involved, such as the core structure and stacking fault energy and others. We also need to consider the effect of incidence angle.
As a result, there are many factors to affect the interaction mechanisms, so that it is very challenging to draw a simple rule to determine the various types of interactions.
There has been many trials to characterize interaction mechanisms from analytical and computational approach, but there still lacks of a general rule. I expect stochasticity would also play a role, but I am not aware of much in detail about it. Other opinion/suggestions on stochasticity will be highly appreciated.
Secondly, I do agree that concurrent modeling approach to model interface would be a good idea to deal with complex interactions, because continuum approach will be helpful to consider large deformation(including rotation) and also give rise to accurate far-field stress calculations. However, it still required a “rule”, which I believe, only comes from atomistic modeling with proper potentials.
How to bridge MD with DD
Dear Ill,
Thank you very much for your posting such impressive topics. As shown in Fig. 4, the deformation mechanisms revealed by DD simulations is very similar to that indicated by MD simulations. But there exists an apparent difference in the length scale between DD and MD simulations. Has there been any method to bridge MD with DD?
Best,
Xiaoyan
Re:How to bridge MD with DD
Thanks for your comments. It is very interesting to get the very similar dislocation structures in DD with MD, with a simple nucleation based on max. resolved shear stress in different oriented micropillars. However, the dislocation network in DD is not exactly the same as MD result. For example, in <100> oriented pillars, MD shows a rectangular network, but DD shows cross-shaped dislocations. I believe both models has limitations to get the “real” structures. That is to say, very high strain rate in MD would localize dislocation activity on a single slip plane, and the dislocation microstructure in DD results from a nucleation rule. I believe it would be needed to perform in-Situ TEM experiments to see the real dislocation structures, but it is also challenging to do torsion experiment in this scale. I look forward to see the experimental proof on anisotropic dislocation microstructures.
Regarding the different time scale in MD and DD, DD results could give rise to very similar stress-strain relations with steady-state experiments via a modified loading condition(so called cut-off plastic strain rate method), while MD has an intrinsic limitation on high strain rate. DD model is required to have atomistic input, in order to characterize individual dislocation mobility and mutual interaction mechanism. Therefore, the scaling bridging between MD and DD would be handled by hierarchical coupling, rather than concurrent approach due to different time scale.
time scale bridging in MD
Dear Ill:
Thanks for bringing up this interesting journal club. Since you mention the well-known time scale issues with MD, I wanted to mention some recent work that has been done in this area with regards to metal plasticity. Specifically, we recently showed that, using potential energy landscape exploration techniques, we can both capture experimentally-observed rate-dependent ductile-to-brittle transitions in bicrystalline metal nanowires:
https://pubs.acs.org/doi/abs/10.1021/acs.nanolett.7b04972
while also predicting new superplastic creep behavior in single crystal metal nanowires that emerges at timescales inaccessible to MD:
https://pubs.acs.org/doi/abs/10.1021/acsnano.8b02199
There are also other groups doing excellent, related work on predictive modeling of different material systems using similar time scale bridging techniques. For example Sid Yip and collaborators on amorphous solids (http://www.pnas.org/content/114/52/13631), and Pradeep Sharma working on a variety of material systems (batteries, metals, etc, i.e. https://journals.aps.org/prmaterials/abstract/10.1103/PhysRevMaterials.1.055401).
Re:time scale bridging in MD
Dear Harold
Thank for your comment and sharing very relevant papers. The strain rate in MD is a long-stranding challenge and many efforts have been made to resolve this limitations. It is very intereting to see your recent work and others, which could achieve physically reasonable time duration in MD modeling.
Another interesting approach to resolve the time step in MD is found from developing special purpose supercomputer for biomolecular simulation designed and constructed by D. E. Shaw Research (DESRES). Without develiping a new algorithm for time-step, they could perform MD simulation for long timespan (https://www.nature.com/articles/nphys3553), which allow us to investigate detailed motion of molecules without losing "jiggling and wiggling" motions of atoms, said Richard Feynman in his seminal 1963 Lectures on Physics.
Dear Ill,
Dear Ill,
Thank you very much for your detailed explanations, which provide important insights to multiscale modelling. The hierarchical coupling you suggested might be effective for bridging between DD and MD, which would advance the understanding of plasticity from atomic level to dislocation level.